please help me answer the following in a step by step process
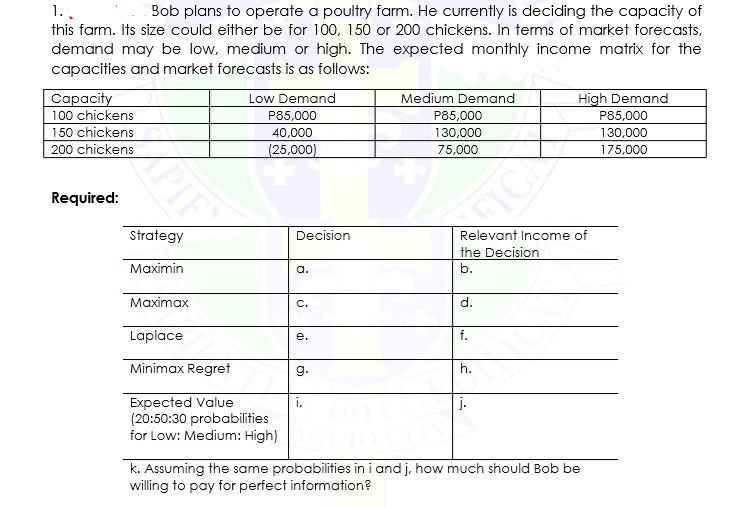
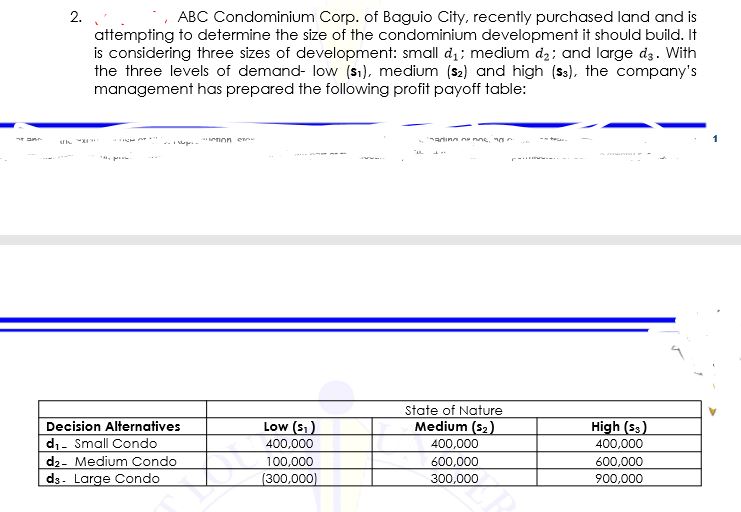
1 . . _Bob plans to operate a poultry farm. He currently is deciding the capacity of this farm. Its size could either be for 100, 150 or 200 chickens. In terms of market forecasts, demand may be low, medium or high. The expected monthly income matrix for the capacities and market forecasts is as follows: Capacity Low Demand Medium Demand High Demand 100 chickens P85,000 P85,000 P85,000 150 chickens 40,000 130,000 130,000 200 chickens 25,000 75,000 175,000 Required: Strategy Decision Relevant Income of the Decision Maximin a. b. Maximax C. d. Laplace e. f. Minimax Regret 9. h. Expected Value i . i. (20:50:30 probabilities for Low: Medium: High) k. Assuming the same probabilities in i and j, how much should Bob be willing to pay for perfect information?2. ABC Condominium Corp. of Baguio City, recently purchased land and is attempting to determine the size of the condominium development it should build. It is considering three sizes of development: small dj; medium d2; and large ds . With the three levels of demand- low (si), medium (sz) and high (ss), the company's management has prepared the following profit payoff table: State of Nature Decision Alternatives Low (S, ) Medium (52) High (53) d1 - Small Condo 400,000 400,000 400,000 d2- Medium Condo 100,000 600,000 600,000 d3- Large Condo (300,000] 300,000 900,0000:3un 1. Assuming the probabilities for the state of nature are 15(51] = 0.2!]; P-{szji = 0.35 and Pris?) = 0.45. 'Whl' decision should ABC Condominium Corp make? 2. What is the relevant income in ABC's decision? 3. At how much will the \"Medium condo. high demand" payoff would be indifferent between the "Medium condo" and "Large condo" decisions, given all other applicable data input items remain the same? Compute for the Expected Value of Perfect Information. Suppose that before making a nal decision. ABC Condominium Corp is considering conducting a survey to help evaluate the demand for the new condominium development. The survey report anticipated to indicate one of the two levels of demand: weak [W] or strong [5]. The relevant probabilities are as follows: P[W|s1} = 0.?5 P[S|s'1) = 0.25 P19\" Pt'ls = st-5 Fflsg} = 0.55 A. What is the expected value with sample information? B. What is the expected value of sample information? C. What is the efficiency of the survey information [present your answer in decimal number NOT percentage for ex: 0.2000 not 20%]