please help me

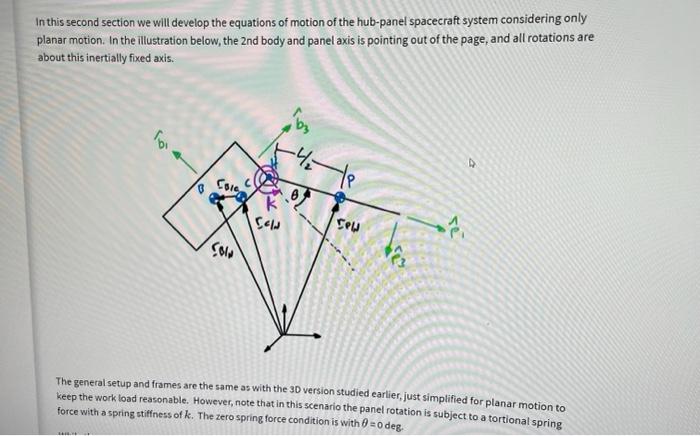
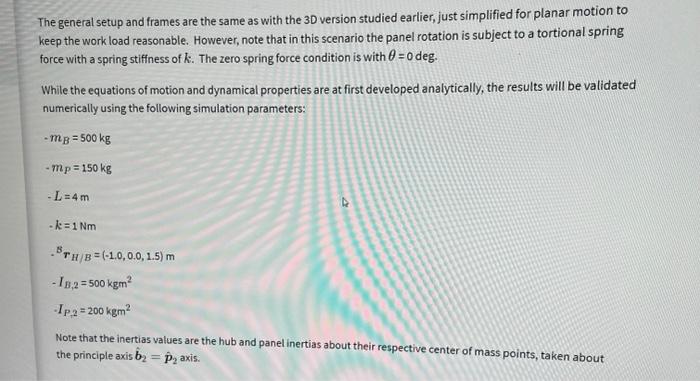
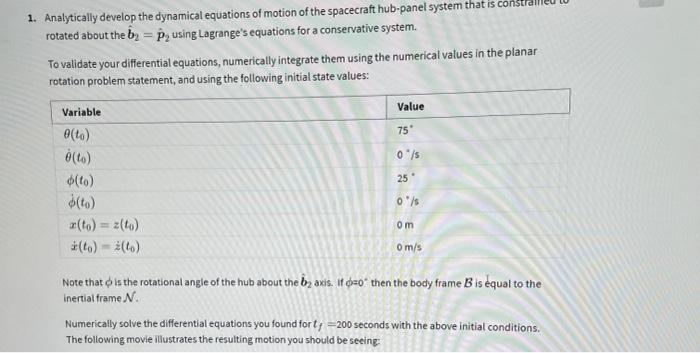
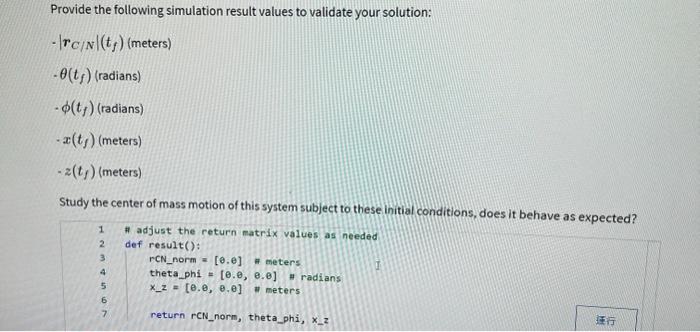
In this second section we will develop the equations of motion of the hub-panel spacecraft system considering only planar motion. In the illustration below, the 2 nd body and panel axis is pointing out of the page, and all rotations are about this inertially fixed axis. The general setup and frames are the same as with the 30 version studied earlier, just simplified for planar motion to keep the work load reasonable. However, note that in this scenario the panel rotation is subject to a tortional spring force with a spring stiffness of k. The zero spring force condition is with =0 deg. The general setup and frames are the same as with the 3D version studied earlier, just simplified for planar motion to keep the work load reasonable. However, note that in this scenario the panel rotation is subject to a tortional spring force with a spring stiffness of k. The zero spring force condition is with =0deg. While the equations of motion and dynamical properties are at first developed analytically, the results will be validated numerically using the following simulation parameters: mB=500kgmP=150kgL=4mk=1NmBrH/B=(1.0,0.0,1.5)mIB,2=500kgm2IP,2=200kgm2 Note that the inertias values are the hub and panel inertias about their respective center of mass points, taken about the principle axis b^2=p^2 axis. 1. Analytically develop the dynamical equations of motion of the spacecraft hub-panel system that is constrdineu tu rotated about the b^2=p^2 using Lagrange's equations for a conservative system. To validate your differential equations, numerically integrate them using the numerical values in the planar rotation problem statement, and using the following initial state values: Note that is the rotational angle of the hub about the b^2 axis. If =0 then the body frame B is equal to the inertial frame N. Numerically solve the differential equations you found for tf=200 seconds with the above initial conditions. The following movie illustrates the resulting motion you should be seeine: Provide the following simulation result values to validate your solution: rC/N(tf)(meters)(tf)(radians)(tf)(radians)x(tf)(meters)z(tf)(meters) Study the center of mass motion of this system subject to these initial conditions, does it behave as expected? \# adjust the return matrix values as needed def result (): rCN_norm =[,] " meters theta_phi =[.,.] " radians xZz=[.,.] in meters return rCN_norm, theta_phi, xz