Please help me!

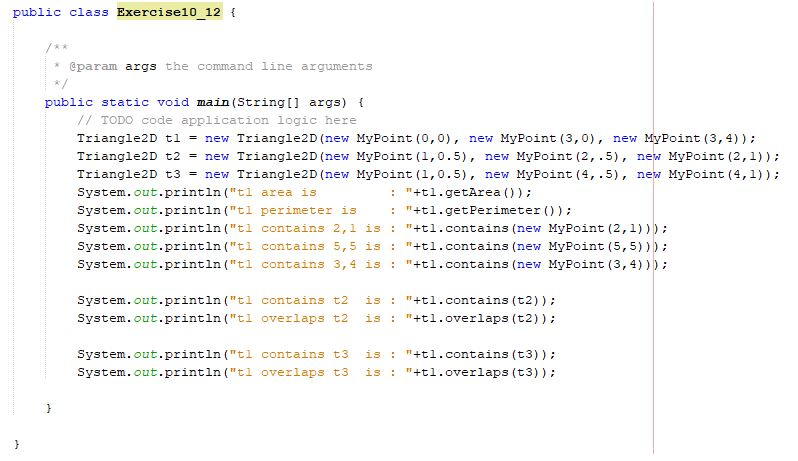
public class Triangle2D { MyPoint p1; MyPoint p2; MyPoint p3; public MyPoint getP1(); { return p1; } public void setP1(MyPoint p1) { this.p1 = p1; } public MyPoint getP2(); { return p2; } public void setP2(MyPoint p1) { this.p2 = p2; } public MyPoint getP3(); { return p3; } public void setP3(MyPoint p3) { this.p3 = p3; } Triangle2D() { p1 = new MyPoint(0.0); p2 = new MyPoint(1.1); p3 = new MyPoint(2.5); } Triangle2D(MyPoint p1, MyPoint p2, MyPoint p3) { this.p1 = p1; this.p2 = p2; this.p3 = p3; } public double getArea(){ double side1 = Math.sqrt(Math.pow(p2.getX() -p1.getX(),2)+Math.pow(p2.getY()-p1.getY(),2)); double side2 = Math.sqrt(Math.pow(p3.getX() -p2.getX(),2)+Math.pow(p3.getY()-p2.getY(),2)); double side3 = Math.sqrt(Math.pow(p1.getX() -p3.getX(),2)+Math.pow(p1.getY()-p3.getY(),2)); double s =(side1 + side2 + side3)/2; double area = Math.sqrt(s * ((s - side1) * (s - side2) * (s - side3))); return area; } public double getperimeter(){ double side1 = Math.sqrt(Math.pow(p2.getX() -p1.getX(),2)+Math.pow(p2.getY()-p1.getY(),2)); double side2 = Math.sqrt(Math.pow(p3.getX() -p2.getX(),2)+Math.pow(p3.getY()-p2.getY(),2)); double side3 = Math.sqrt(Math.pow(p1.getX() -p3.getX(),2)+Math.pow(p1.getY()-p3.getY(),2)); double perimeter = side1 + side2 + side3; return perimeter; } public boolean contains(MyPoint p){ double[][]points = new double[4][2]; points[0][0]=this.p1.getX(); points[0][1]=this.p1.getY(); points[1][0]=this.p2.getX(); points[1][1]=this.p1.getY(); points[2][0]=this.p2.getX(); points[2][1]=this.p1.getY(); points[3][0]= p.getX(); points[3][1]= p.getX(); if (getIntersectingPoint(points)! = null) { return true; } return false; } public boolean contains (Triangle2D t){ if((this.getArea()>t.getArea())) { return true; } else { return false; } } public boolean overlaps (Triangle2D t){ double[][]points = new double[4][2]; points[0][0]=this.p1.getX(); points[0][1]=this.p1.getY(); points[1][0]=this.p2.getX(); points[1][1]=this.p1.getY(); points[2][0]=this.p2.getX(); points[2][1]=this.p1.getY(); points[3][0]= t.p1.getX(); points[3][1]= t.p1.getY(); int count = 0; if(getIntersectingPoint(points)!=null){ count ++; } points[3][0] = t.p2.getX(); points[3][1] = t.p2.getY(); if(getIntersectingPoint(points)!=null) { count ++; } points[3][0] = t.p3.getX(); points[3][1] = t.p3.getY(); if(getIntersectingPoint(points)!=null) { count++; } if(count>1) return true; return false; } public double[] getIntersectingPoint(double[][] points){ double y12 = points[0][1] - points[1][1]; double x12 = -(points[0][0] - points[1][0]); double y34 = points[2][1]- points[3][1]; double x34 = -(points[2][0] - points[3][0]); double b0 = (points[0][1] - points[1][1])*points[0][0] - (points[0][0] - points[1][0]) * points[0][1]; double b1 = (points[2][1] - points[3][1]) * points[2][0] - (points[2][0] - points[3][0]) * points[2][1]; double denom = y12 * x34 - x12 *y34; if(denom == 0) { return null; } double[] intersectingPoint = new double[2]; intersectingPoint[0] = (b0 * x34 - x12 * b1)/denom; intersectingPoint[1] = (y12 * b1 - b0 * y34)/denom; return intersectingPoint; }

10.12 (Geometry the Triangle2D class) Define the Triangle2D class that contains: Three points named pl, p2, and p3 of the type MyPoint with getter and setter methods. MyPoint is defined in Programming Exercise 10.4 A no-arg constructor that creates a default triangle with the points (0, 0), (1 1), and (2, 5). A constructor that creates a triangle with the specified points. A method getArea that returns the area of the triangle A method getPerimeterO that returns the perimeter of the triangle A method contains (MyPoint p) that returns true if the specified point p is inside this triangle (see Figure 10.22a). A method contains (Triangle2D t) that returns true if the specified triangle is inside this triangle (see Figure 10.22b). A method overlaps (Triangle2D t) that returns true if the specified triangle overlaps with this triangle (see Figure 10.22c). FIGURE 10.22 (a) A point is inside the triangle. (b) A triangle is inside another triangle (c) A triangle overlaps another triangle. Draw the UML diagram for the class and then implement the class. Write a test program that creates a Triangle2D objects t1 using the constructor new Triangle2D(new MyPoint (2.5, 2), new MyPoint(4.2, 3), new MyPoint(5, 3.5)), displays its area and perimeter, and displays the result of tl.contains(3, 3), r1.contains (new Triangle2D Cnew MyPoint (2.9, 2), new MyPoint(4, 1), MyPoint(1, 3.4))), and t1. overlaps (new Triangle2D(new MyPoint (2, 5.5), new MyPoint (4, -3), MyPoint (2, 6.5))). (Hint: For the formula to compute the area of a triangle, see Programming Exer cise 2.19. To detect whether a point is inside a triangle, draw three dashed lines, as shown in Figure 10.23. If the point is inside a triangle, each dashed line should intersect a side only once. If a dashed line intersects a side twice, then the point must be outside the triangle. For the algorithm of finding the intersect- ing point of two lines, see Programming Exercise 3.25.)