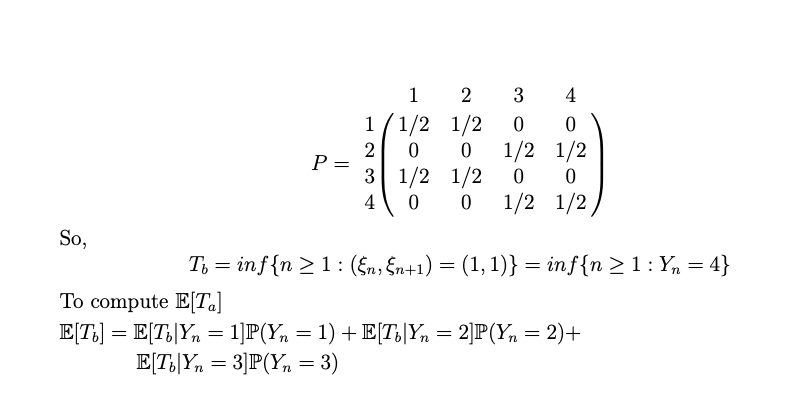
Please help me to compute E[T_c] and E[T_d]

2. Suppose that {En}nzo is a sequence of independent and identically distributed random varia- bles such that En Bernoulli(1/2). Compute: a) E[T.) with Te = inf{n> 1: (En; &n+1, 6n+2) = (1, 1, 1)}. Let W. be a random variable such that 3 4 si (En, En+1; &n+2) = (0,0,0) 2 si (En, En+1; &n+2) = (0,0,1) si (En; &n+1, 6n+2) = (0,1,0) si (En, En+1, En+2) = (0,1,1) Wn= 5 si En &n+1;&n+2) = (1,0,0) 6 si (En&n+1; &n+2) = (1,0,1) 7 En $n+1, $n+2) = (1,1,0) si (En, &n+1, &n+2) = (1,1,1) so, {Wh:n >0} is Markov Chain with = = {1, 2, 3, 4, 5, 6, 7, 8} and transition probability matrix P given by 00 1 2 3 4 5 6 7 8 1 1/2 1/2 0 0 0 0 0 0 2 0 0 1/2 1/2 0 0 0 3 0 0 0 0 1/2 1/2 0 0 4 0 0 0 0 0 0 1/2 1/2 P= 5 1/2 1/2 0 0 0 0 0 0 6 0 0 1/2 1/2 0 0 0 0 7 0 0 0 0 1/2 1/2 0 0 8 0 0 0 0 0 0 1/2 1/2 so, Te = inf{n> 1 : En. n+1, 6n+2) = (1,1,1)} = inf{n> 1:W. = 8} E[Te] = E(TcWn = 1]P(Wn = 1) + E[TcWn=2]P(Wn = 2)+ E[TcWn = 3]P(Wn = 3) + E[TcWn = 4]P(W1 = 4)+ E[T_W, = 5]P(Wn = 5) + E[TcW, = 6]P(Wn = 6)+ E[TW. = 7]P(W. = 7) + ETW. = 8]P(W. = 8) b) E[Ta] with Ta = inf{n> 1 : (En, En+1) = (1,0)}, Let Yn be a random variable such that Yn si si si si 3 (En, &n+1) = (0,0) (En, En+1) = (0,1) (En, &n+1) = (1,0) (En, &n+1) = (1,1) {1,2,3,4} and transition probability matrix P 4 {Ynin >0}is a Markov chain with = given by 1 2 3 4 1/1/2 1/2 0 0 2 0 0 1/2 1/2 P= 3 1/2 1/2 0 0 4 0 0 1/2 1/2 So, T = inf{n > 1: (En, &n+1) = (1, 1)} = inf{n>1:Yn = 4} To compute E[Ta] E[TG] = E(TYn = 1]P(Yn = 1) + E[T. Yn = 2]P(Yn = 2)+ E[T6|Yn = 3]P(Yn = 3) = 2. Suppose that {En}nzo is a sequence of independent and identically distributed random varia- bles such that En Bernoulli(1/2). Compute: a) E[T.) with Te = inf{n> 1: (En; &n+1, 6n+2) = (1, 1, 1)}. Let W. be a random variable such that 3 4 si (En, En+1; &n+2) = (0,0,0) 2 si (En, En+1; &n+2) = (0,0,1) si (En; &n+1, 6n+2) = (0,1,0) si (En, En+1, En+2) = (0,1,1) Wn= 5 si En &n+1;&n+2) = (1,0,0) 6 si (En&n+1; &n+2) = (1,0,1) 7 En $n+1, $n+2) = (1,1,0) si (En, &n+1, &n+2) = (1,1,1) so, {Wh:n >0} is Markov Chain with = = {1, 2, 3, 4, 5, 6, 7, 8} and transition probability matrix P given by 00 1 2 3 4 5 6 7 8 1 1/2 1/2 0 0 0 0 0 0 2 0 0 1/2 1/2 0 0 0 3 0 0 0 0 1/2 1/2 0 0 4 0 0 0 0 0 0 1/2 1/2 P= 5 1/2 1/2 0 0 0 0 0 0 6 0 0 1/2 1/2 0 0 0 0 7 0 0 0 0 1/2 1/2 0 0 8 0 0 0 0 0 0 1/2 1/2 so, Te = inf{n> 1 : En. n+1, 6n+2) = (1,1,1)} = inf{n> 1:W. = 8} E[Te] = E(TcWn = 1]P(Wn = 1) + E[TcWn=2]P(Wn = 2)+ E[TcWn = 3]P(Wn = 3) + E[TcWn = 4]P(W1 = 4)+ E[T_W, = 5]P(Wn = 5) + E[TcW, = 6]P(Wn = 6)+ E[TW. = 7]P(W. = 7) + ETW. = 8]P(W. = 8) b) E[Ta] with Ta = inf{n> 1 : (En, En+1) = (1,0)}, Let Yn be a random variable such that Yn si si si si 3 (En, &n+1) = (0,0) (En, En+1) = (0,1) (En, &n+1) = (1,0) (En, &n+1) = (1,1) {1,2,3,4} and transition probability matrix P 4 {Ynin >0}is a Markov chain with = given by 1 2 3 4 1/1/2 1/2 0 0 2 0 0 1/2 1/2 P= 3 1/2 1/2 0 0 4 0 0 1/2 1/2 So, T = inf{n > 1: (En, &n+1) = (1, 1)} = inf{n>1:Yn = 4} To compute E[Ta] E[TG] = E(TYn = 1]P(Yn = 1) + E[T. Yn = 2]P(Yn = 2)+ E[T6|Yn = 3]P(Yn = 3) =