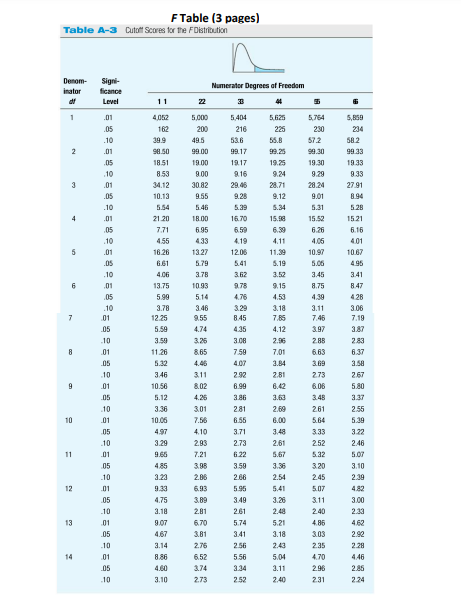
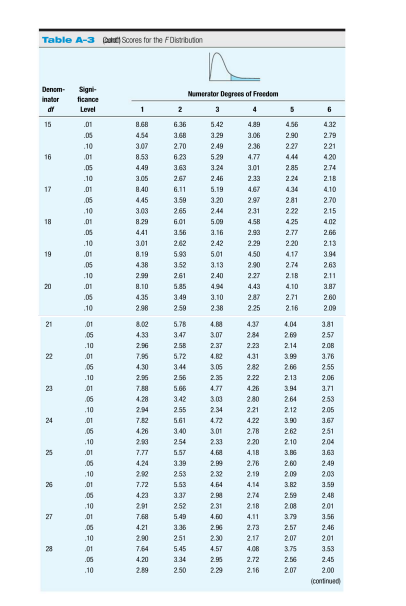
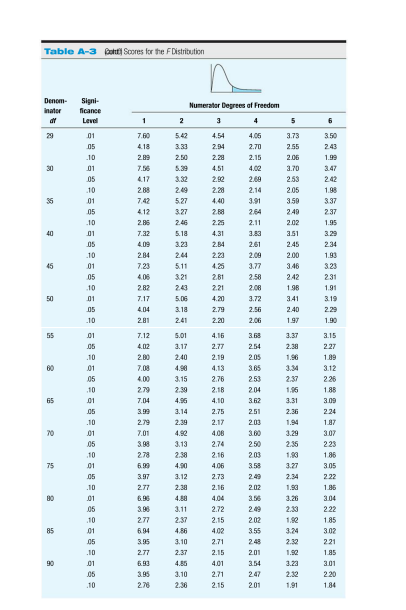
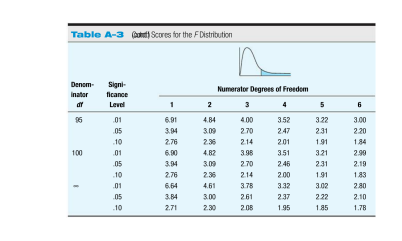
Please help me understand this concept. I need explanations on how do these. thank you

Q3. Proportions (percentages) in a Z Distribution [10 points]

A standardized visual working memory test has a population mean (?) of 54 and a standard deviation (?) of 4. Because the scores are normally distributed, the whole distribution of scores can be converted into a Z distribution. Each raw score in the original distribution has a corresponding Z score in the Z distribution. The Z distribution has a symmetrical bell shape with known properties, so it's possible to mathematically figure out the percentage of scores within any specified area in the distribution.

Deduct 0.5 if the calculation process is correct but the result is wrong

Helpful tips:

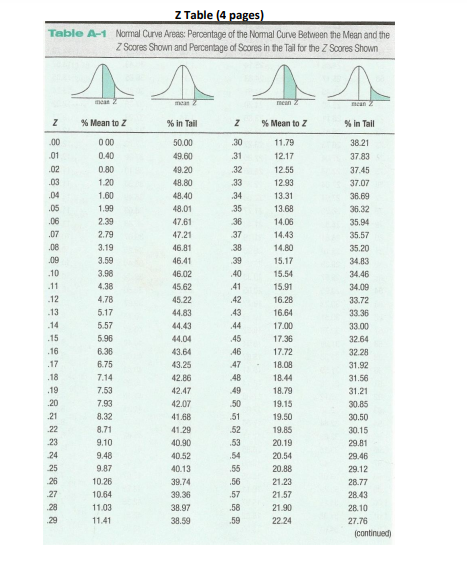
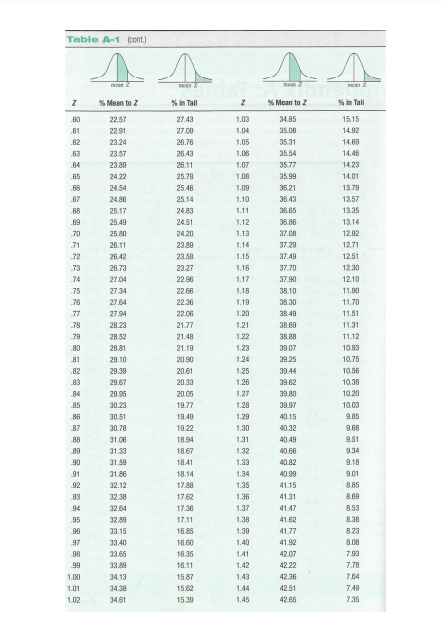
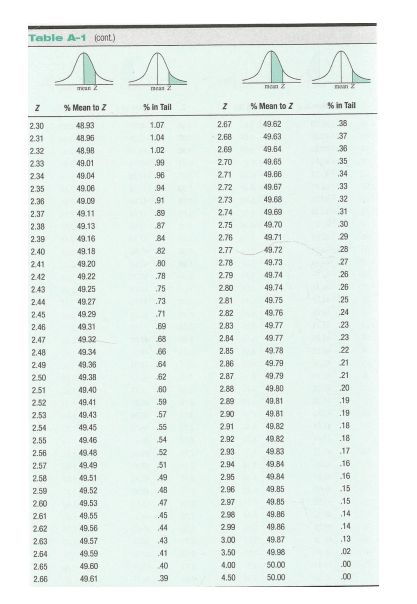
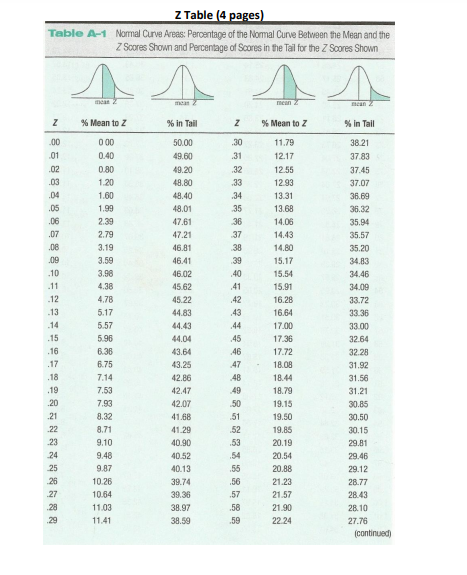
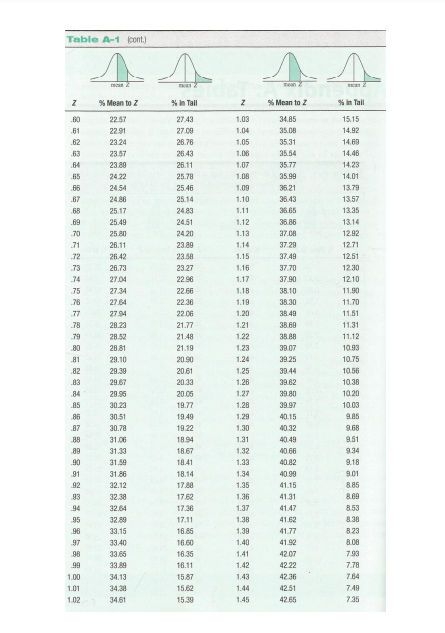
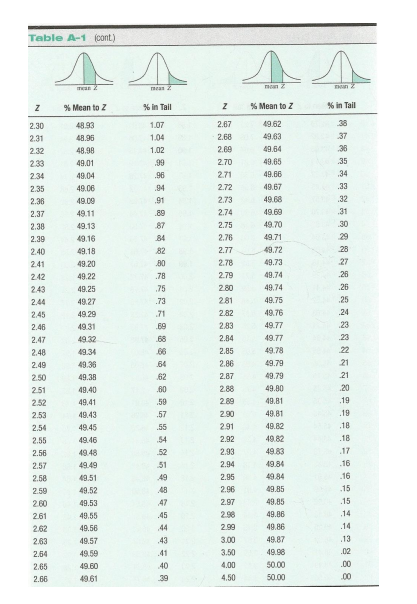
To answer the following questions, it helps to draw a Z distribution (bell curve) and place an individual's Z score on the distribution as a visual aid. Use the Z table for converting between Z score and area (percentage) of the distribution marked by this Z score

Use this Normal Distribution Table to visualize how your z scores are plotted on a normal distribution:

https://www.mathsisfun.com/data/standard-normal-distribution-table.html

.

Q3 A. Raven has a score of 47. What is Raven's Z score? Round the result to the hundredth (2^nd place to the right of the decimal).

[1 point]

Z = (X-m)/s *Population Mean =m *Population Standard Deviation =s

*Raw Score = X *Z score =Z

Z= (X-M)/SD

Z= (47 - 54)/4

Z= -7/4

Z= -1.75

Q3 B. What is the percentage of students that score lower than Raven?

[1 point]

Q3 C. Based on the Z table, if 1000 students take the test, how many of them would likely scoreabove Raven's score? (Round the answer to a whole number)

[1 point]

Q3 D. Erica has a score of 59. What is Erica's Z score?

[1 point]

Z = (X-m)/s *Population Mean =m *Population Standard Deviation =s

*Raw Score = X *Z score =Z

Z= (X-M)/SD

Z= (59 -54)/4

Z= 5/4

Z= 1.25

Q3 E. What is the percentage of students that score lower than Erica?

[1 point]

Using the standard deviation table 0 to 1.25 is 39.44%. Each side of the table is 50%. So 50% add 39.44 and you can see everyone bellow that point.

39.44+ 50=

89.44% of people score lower than Erica

P== 0.894

Q3 F. Based on the Z table, if 1000 students take the test, how many of them would likely scorebelowErica's score? (Round the answer to a whole number)

[1 point]

Q3 G. What is the percentage of students that score between Raven and Erica?

[1 point]

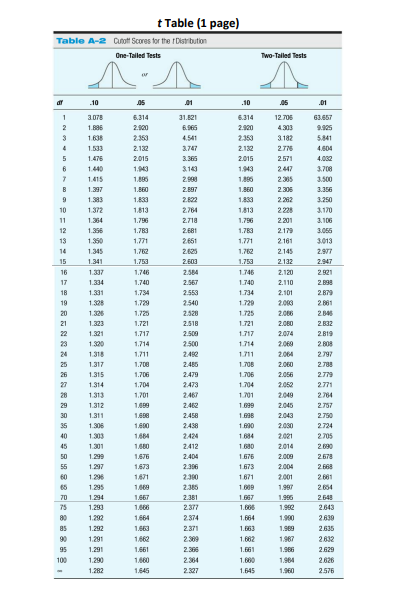
Q3 H. Ryan scores at the 78^th percentile on this exam, what is his Z score?

Hint: A score at 78^th percentile means 78% of the scores are below this score.

[1 point]

Q3 I. Based on the result of the previous question and using the population mean and SD for Q3, what is Ryan's raw score of working memory?

[1 point]

Q3 J. What would be the median raw score on this exam?

Hint: Review the definition of "median" and then figure out the percentage of scores below (or above) this score.

[1 point]

Q4. Z Distribution: From Probabilities to Proportions (percentages)[7 points]

Answer the following questions with this scenario:

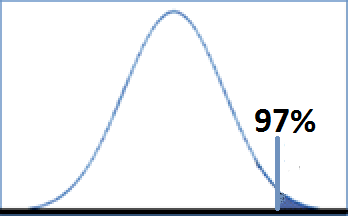
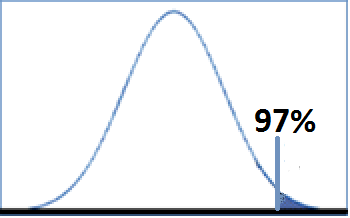
A school district runs a gifted language program in fourth grade with a selection criterion of 97^th percentile. That is, students who score at 97^th percentile or above on a standardized language test are eligible for the gifted program. Answer the following question based on this scenario.

Helpful tips:

Review the tutorial videos on "how to use the Z table" before answering the following questions.

\fTam- 1H 1m; 44.; 4A : 51.111111: 11m\" I Fla-1'2 \"In 2311 is: 1111' w 111m 1: 2.3.1 111111 1.01 2511 41m .111 2.32 411.111 1112 :31; man as La: 111111 .1111 111: 11111.1 3: 2.11- 19111 .1111 :11 19155 .31 235 111.1111 .111 112 m1? .3: 2.1111 49.1111 .11 2.13 was .32 2.117 13.11 m 2.71 was .31 2.31 m: .91 2.15 19.10 53 no 19.16 11: 2.111 11.11 , 211 2.111 19.111 .112 m _ _ ,_ 11.72 .121 2.41 191211 30 2.13 111.1: :1 1+2 4112': .111 1111 111.111 211 2113 11125 .1! 2.11: 411.14 .1311 LII an .13 1.01 11175 .25 1.1.1 11129 .11 1112 11m .3 m 1931 .311 2.113 11?? .23 24? an m \"I dam 22 2.11. am a 2115 an 22 219 11.35 1111 1:33 13.111 41 w 111.11! .112 21.7 1.111 :21 2.111 1111411 1111 2111 41m 111 2.112 111.11 .1111 La! 4911 19 2.51; 4111-15 .5? 25:1 4m .19 2.51 111.111 55 2.91 am .1 a 2.11! M .51 2112 11m .13 2.511 49.10 a 2.1111 45.3: .11 2.5? u .51 2114 an .111 2.511 41.51 .19 2115 11.114 .15 251! 111.4312 .111 2.3 111.1111 1a 2.93 19.511 .11 m M 15 7.131 11111 .15 1111 5111111 11 2.11:: 19153 .14 2.31 11m 111 2113 11151 .4; 1111 111.11? 13 9.11: ms .41 3.1111 mm 112 1111 an: .11: m: 111m 111 2.311 MI .3! 1.11} sum .00 \fF Table (3 pages) Table A-3 Cutof Scores for the FDistribution Demom- Sign- Numerator Degrees of Freedom inator licance Level 11 22 4 052 5.000 5.404 5.625 5.764 5,839 .05 162 200 216 225 230 234 .10 49 5 57.2 99 00 98.17 93.26 94.30 EE 65 .05 18.51 15 00 1917 1933 10 8.53 0.16 9.24 3.29 9 33 .01 34.12 30 82 29. 4 24.71 28.24 27 9 .05 10.13 9 55 9.24 9.12 9.01 .10 5.54 5.39 6.34 1.31 5.28 21 20 18 00 16.70 15.10 15.52 15.21 105 7.71 695 6.50 8 16 10 1.55 4 33 1.19 4.11 1.05 4 01 5 .01 16.26 13 27 12.06 11.39 10.87 1087 6.61 6 79 5.41 4.19 6.08 4.95 .10 378 3.62 3.52 3.45 3.41 .01 13.75 1093 9.15 R 47 .05 5.99 5.14 4.76 4.53 1.39 4 28 .10 3.78 3.48 3.29 3.18 3.11 3.06 01 12 25 9.55 8 45 7.46 7.19 05 5.59 4.74 4.35 4.12 3.97 3.47 -10 3.26 3.OR 2.06 2.85 2.83 01 11.28 8.85 7.58 7.01 6.83 8.37 6.32 3.84 10 3.46 311 2 92 7.81 2.73 2.67 01 10.56 5.02 6.99 8.42 6.06 5.80 .05 5.12 4.25 3.86 3.63 3.45 3.37 -10 3.36 3.01 281 2/69 261 2.55 01 10.06 7.68 6.55 6.00 5.64 5.39 05 457 4.10 3.71 3.49 3.33 3.72 10 3.29 2.83 2.73 2.61 252 2.48 11 .01 9.65 7.21 6.22 6.67 3.32 5.07 05 1.85 3.95 3.59 3.36 3.20 3.10 .10 3.20 2. DE 2.86 2.54 245 2.19 01 9.33 5.95 5.41 S.07 4.32 05 1.75 3.89 3.48 3.26 3.11 3.00 -10 3.18 2.81 2.61 2.40 240 2.23 13 01 9 07 6.70 5.74 5.21 4.85 4.62 05 4.67 3.81 3.41 3.18 3.03 2.22 -10 3.14 2.76 2.56 2.43 2.35 2.2H 14 01 8.86 652 5.56 5 04 4 70 4 48 05 4.40 3.74 3.14 3.11 2.98 2.45 10 3.10 2.73 2.52 2.40 231 2.24Table A-3 Quit Scores for the FDistribution Denom- Sign Numerator Degrees of Freedom inator Level 1 2 3 G H.GB G.36 6.42 4.89 4 32 4.14 3.29 3.06 2.90 2.79 .10 3.07 2.70 2.48 2.27 2 21 8.53 6.23 5.29 4.77 4 44 4 20 .05 4.49 3.63 3.24 3.01 2.85 2.74 .10 SD'E 2 67 2.46 2.23 2.24 2.18 1.40 6.11 5.19 4:34 4 10 4.45 3.58 3.20 2.97 2.81 2.70 ,10 3.03 2.65 2.31 2.32 2 15 18 GEB 6.01 5.09 4.58 4.25 4 02 4.41 3.56 2.93 2.77 .10 3.01 2.12 2.42 2.29 2.20 2.13 19 .01 8.18 5.93 5.01 4.50 4.17 3.9 4:38 3.52 3.13 2.40 2.74 .10 2.90 2.61 2.40 2.27 2.18 211 20 8.10 6.85 4.94 4.43 4.10 4.35 3.49 3.10 2.47 2.71 260 ,10 2.98 2.50 2.38 2.25 2.16 2 09 21 5.78 4.17 1,04 3.81 347 3.07 2.84 2.57 10 2.06 258 2.37 2.23 2.14 2.08 22 5.72 4. 12 4.31 1.89 3.76 3.44 2.42 2. 68 2.55 10 2.06 2.56 2.35 2.22 2.13 2106 4.26 3.94 3.71 4.28 342 2.80 2.53 .10 2.04 2.55 2.34 231 212 2.05 24 7.42 5.61 4.72 4.22 3.90 3.GT 4.28 3.40 2.76 2.62 2.51 254 2.37 2.30 2.10 204 7.17 4. Fa 4.18 3.BG 4.24 3:39 2 49 2.76 2.60 2.49 ,10 253 2.18 20 26 7.72 5.53 1.64 4.14 3. 82 GUE 4.20 2.74 2.59 2.40 ,10 252 231 2.18 208 201 27 7.68 5.49 4.60 4.11 3.79 3.56 4.21 3:36 2.73 2.57 2.46 .10 2:90 251 2.30 2.17 2.07 2.01 5.45 4.57 3.75 4.20 FEE 2.9% 2.72 2. 56 2.45 10 2.60 2.50 2.29 2.16 207 2.00 (continued\fTable A-3 Call Sops for the FDistribution Denom= Signi- Numerator Degrees of Freedom inator Icance Level 2 3 4 5 6 01 4.84 4 00 352 3.00 05 4.04 2 70 2 AT 2 31 10 7.76 2.35 2 14 201 191 1.84 01 4.R7 351 371 05 2 70 2 46 2.19 10 2.35 214 200 1.83 .01 3 75 3.32 3.02 2.30 .05 3.F1 251 237 2.10 -10 2.71 2.30 205 1.95 1.85 1.78