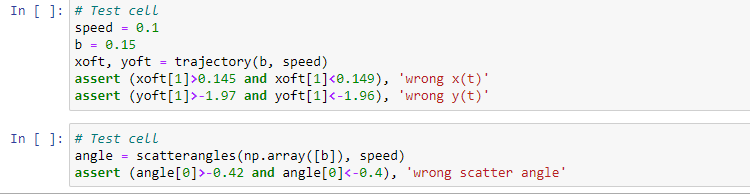
Please help. The code also has to pass both the tests above as well.

Question 11: Pinball scattering is a purely Newtonian equations of motion exercise without feedback or random numbers but showing chaotic behaviour regardless. Consider the potential V(x,y)=x2y2e(x2+y2) (all terms dimensionless) with four maxima centred at x=1 and y=1, respectively. It is defined as a repulsive potential for any test particle (the pinball) moving through that potential. The equations of motion to solve hence are and dt2d2x(t)=2.0y2x(1x2)e(x2+y2) dt2d2y(t)=2.0x2y(1y2)e(x2+y2) Task: Solve these two coupled ODE's in stages: (a) write a function trajectory(impactpar, speed) which takes the impact parameter, x(0), as input as well as the speed vy for initial conditions (impact parameter =x(0),vx=dtdx(0),y(0) and vy=dtdy(0) in that order). Calculate the time array to solve for from np.linspace (, maxtime, 30) where maxtime works well as 10 / speed. The function shall return the trajectory, i.e. the arrays of solved x(t) and y(t) separately. Plot a trajectory of your choice, see below, with appropriate axes labels. As initial values, fix vx=dtdx(0)=0.0 and y(0)=2 (away from the potential in y ). The range of sensible initial values for x(0), should be between 0.9x(0)0.9 but values around 0.10.2 are quite interesting to observe. Likewise, pick a kinetic energy in form of an initial speed 00.145andxoft[1]1.97andyoft[1].42 and angle []<.4 scatter angle>