please help

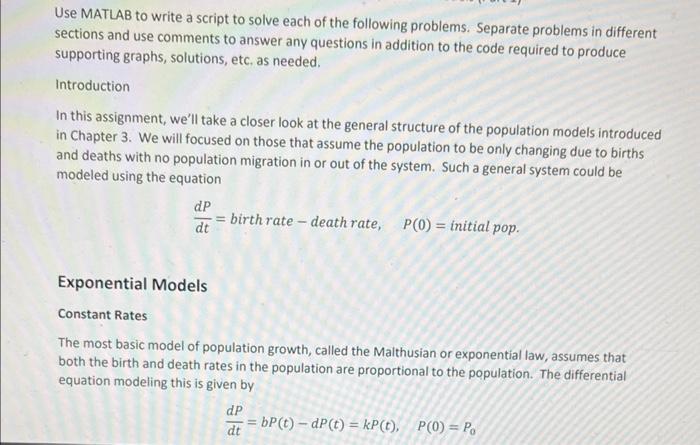
Use MATLAB to write a script to solve each of the following problems. Separate problems in different sections and use comments to answer any questions in addition to the code required to produce supporting graphs, solutions, etc, as needed. Introduction In this assignment, we'll take a closer look at the general structure of the population models introduced in Chapter 3. We will focused on those that assume the population to be only changing due to births and deaths with no population migration in or out of the system. Such a general system could be modeled using the equation dtdP=birthratedeathrate,P(0)=initialpop. Exponential Models Constant Rates The most basic model of population growth, called the Malthusian or exponential law, assumes that both the birth and death rates in the population are proportional to the population. The differential equation modeling this is given by dtdP=bP(t)dP(t)=kP(t),P(0)=P0 Problem 1: Pick a value for k between 0.10 and 0.10, and a value for P(0)=P0 that seems. reasonable for some population that we could be modeling. Then use the dsolve command in MATLAB to solve this equation. - Use syms P(t) to define a symbolic variable t and a function P of that variable - Define the differential equation shown above, as well as your initial condition - Use the dsolve command to find the solution. Type the solution in as a comment after the dsolve command. - Use ezplot to graph the solution. Choose a range of values that seem appropriate so that the exponential graph can be easily seen. You may have to try a few different combinations. You can specify the window in the ezplot command: explot(function, [xmin xmax ymin ymax]]. Note the lack of commas between the window values. Birth Rates Proportional to the Population The next model we'll be looking at assumes that the birth rate is growing proportionally with the square of the population. To make things easier, let's assume that the death rate is 0 , which could be feasible if there are no natural predators and the lifespan of the population members is long relative to the timespan we're measuring over). In this case, the model will simplify to dtdP=kP20=kP2 where k>0 is the rate at which the birth rate increases