Please help!
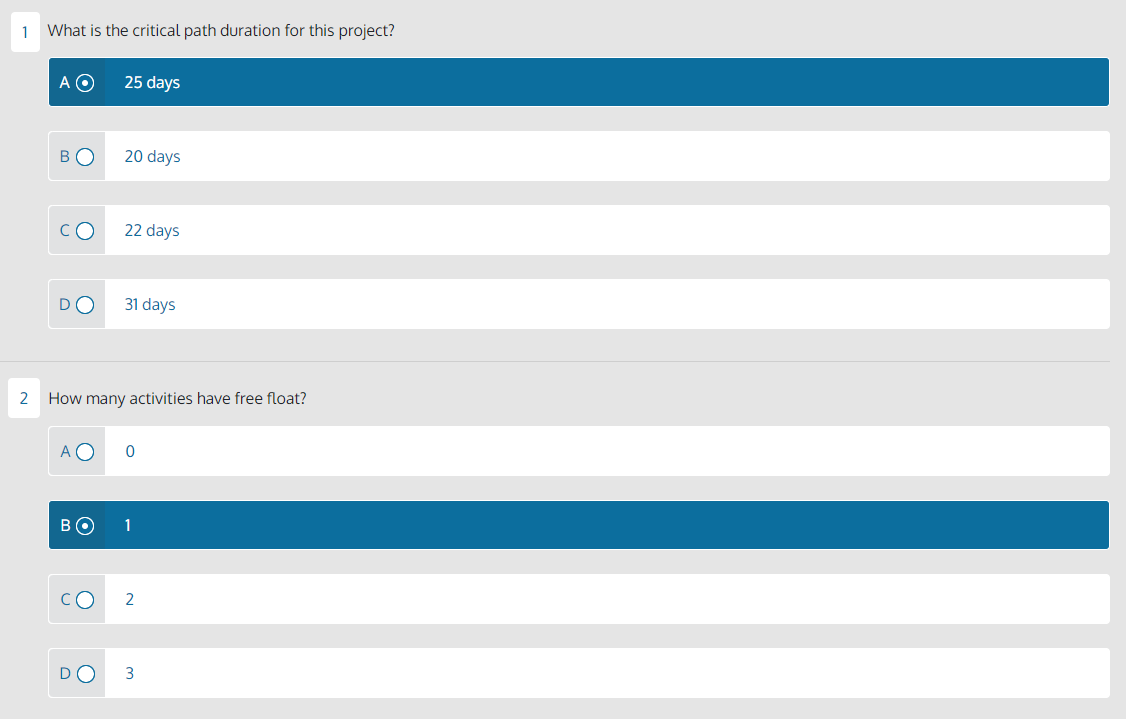
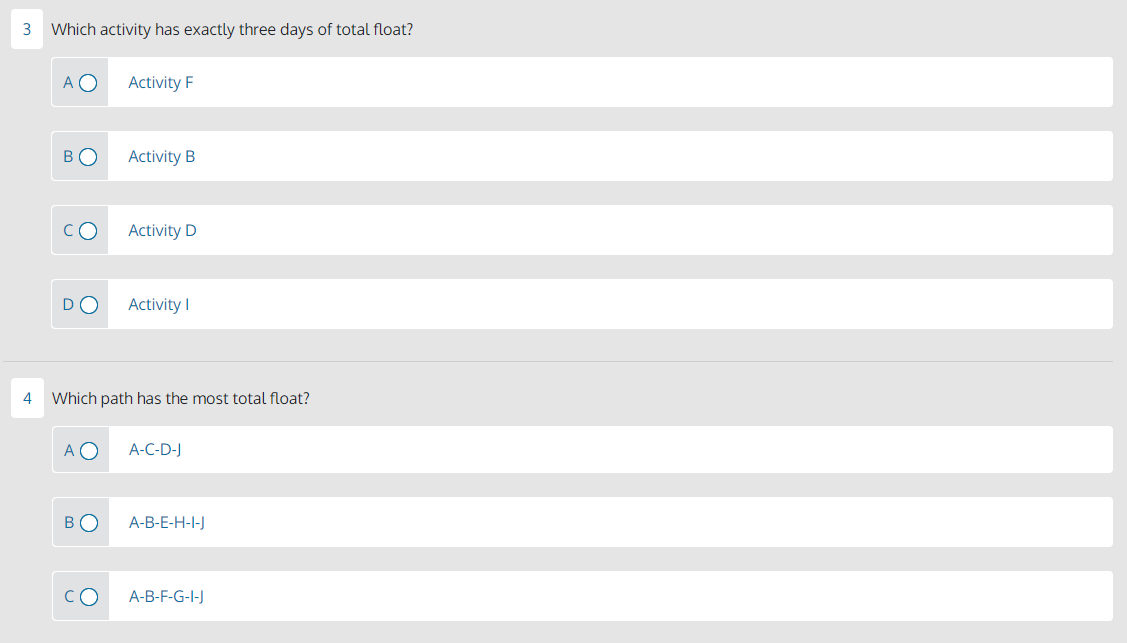
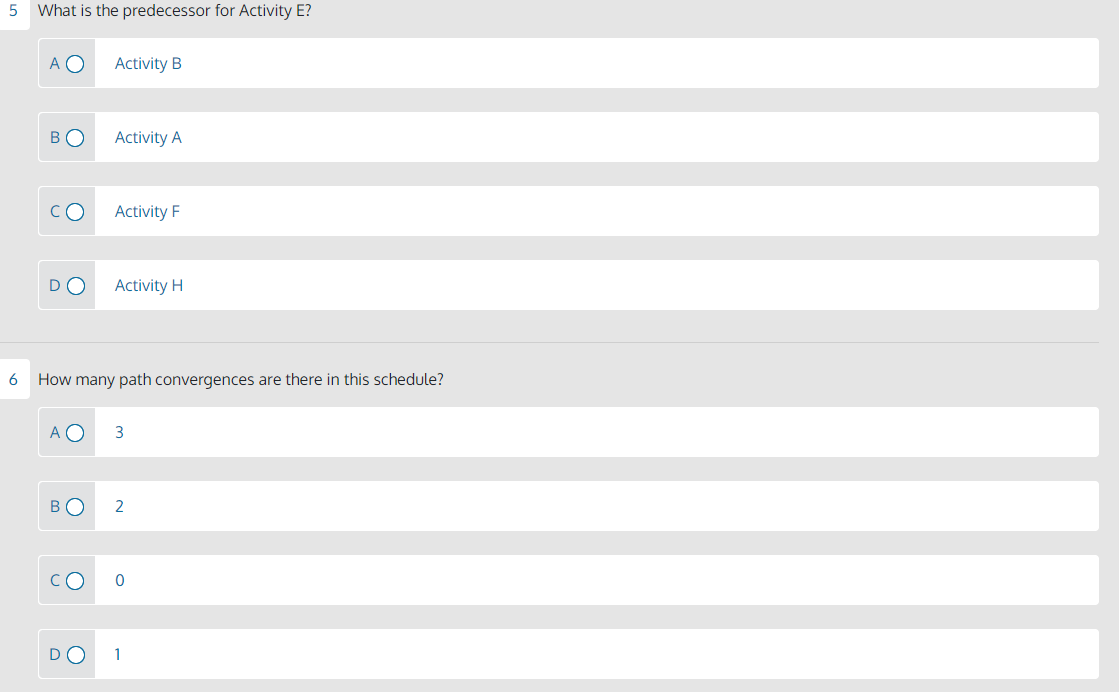
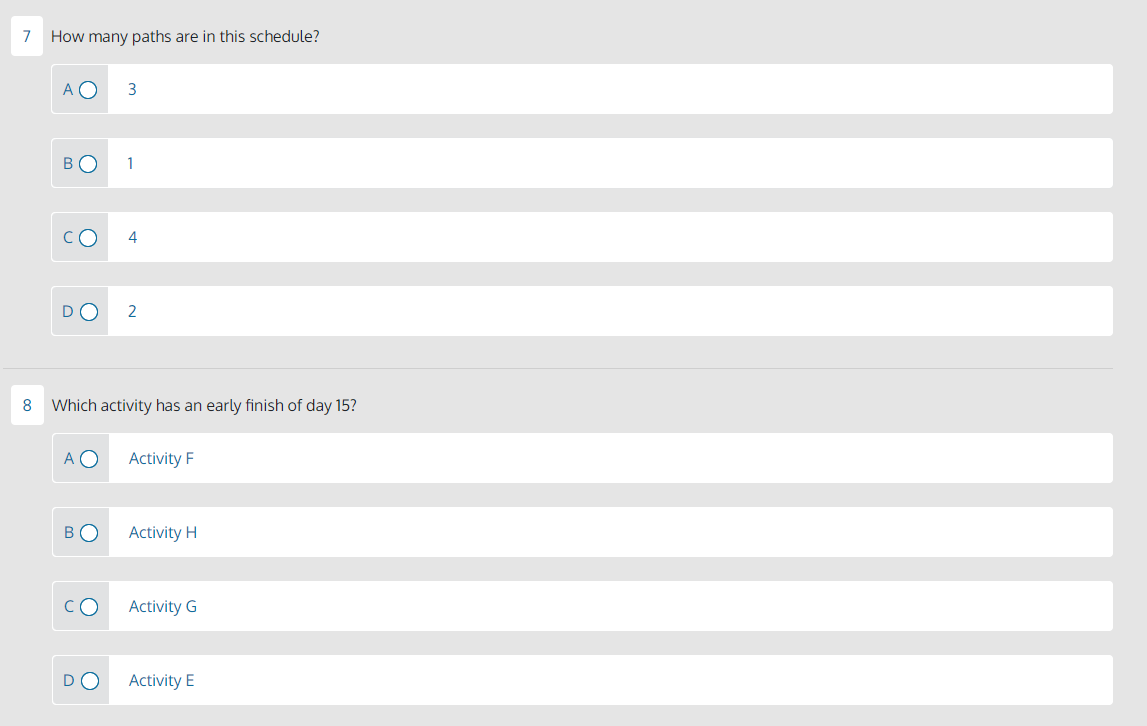
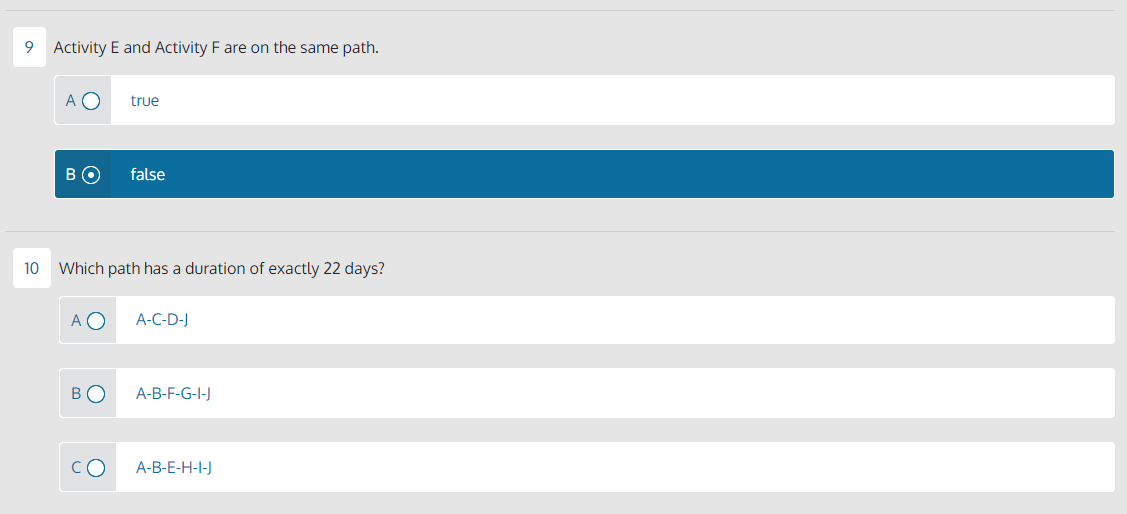

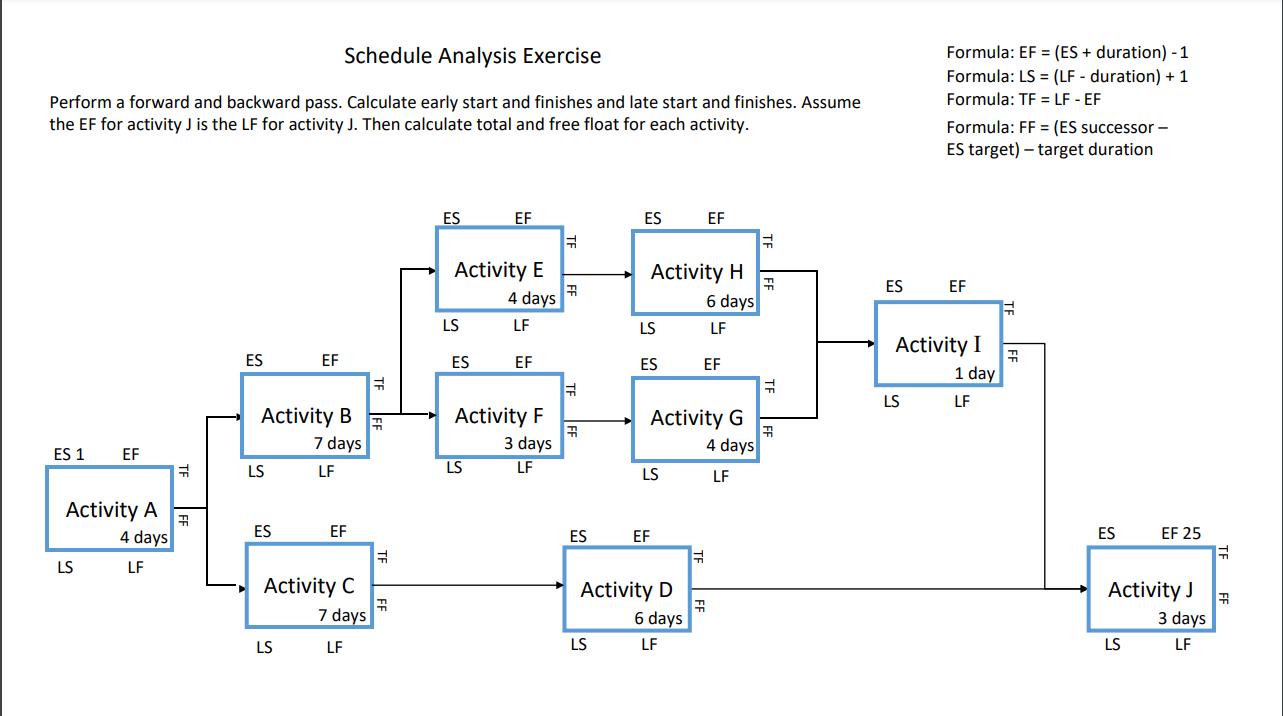
What is the critical path duration for this project? A 25 days 22 days 31 days How many activities have free float? 0 B 1 2 3 Which activity has exactly three days of total float? Activity F Activity B Activity D Which path has the most total float? A-C-D-J ABEHIJ A-B-F-G-I-J What is the predecessor for Activity E? A Activity B B Activity A Activity F D Activity H How many path convergences are there in this schedule? 3 B 2 0 D 1 7 How many paths are in this schedule? 3 4 2 8 Which activity has an early finish of day 15 ? Activity F Activity H Activity G Activity E 9 Activity E and Activity F are on the same path. true B false 10 Which path has a duration of exactly 22 days? AA-C-D-J E A-B-F-G-I-J A-B-E-H-I-J Important Note: This page provides text equivalent for the network diagram shown on the page 1. If you're using screen reader assistant, please view this page instead. Schedule Analysis Exercise Perform a forward and backward pass using the network diagram and formulas below. Calculate all early start and finishes and all late start and finishes. Assume the EF for activity J is the LF for activity J. Then, calculate total and free float for each activity. Formulas: EF=(ES+duration)1LS=(LFduration)+1TF=LFEFFF=(ESsuccessorEStarget)targetduration Network Diagram: - Activity A has a duration of 4 days, an early start of day 1. - On the upper path, Activity B has a duration of 7 days. - On one path from Activity B, Activity E has a duration of 4 days. Activity H has a duration of 6 days. - On the other path from Activity B, Activity F has a duration of 3 days. Activity G has a duration of 4 days. - Both upper paths go to Activity I, which has a 1 day duration. - On the lower path, Activity C has a duration of 7 days. Activity D has a duration of 6 days - The final activity for both paths, Activity J, has a duration of 3 days, an early finish of day 25. Schedule Analysis Exercise Formula: EF=(ES+ duration )1 Formula: LS=(LF duration )+1 Perform a forward and backward pass. Calculate early start and finishes and late start and finishes. Assume the EF for activity J is the LF for activity J. Then calculate total and free float for each activity. Formula: FF= (ES successor













