please help! will upvote!
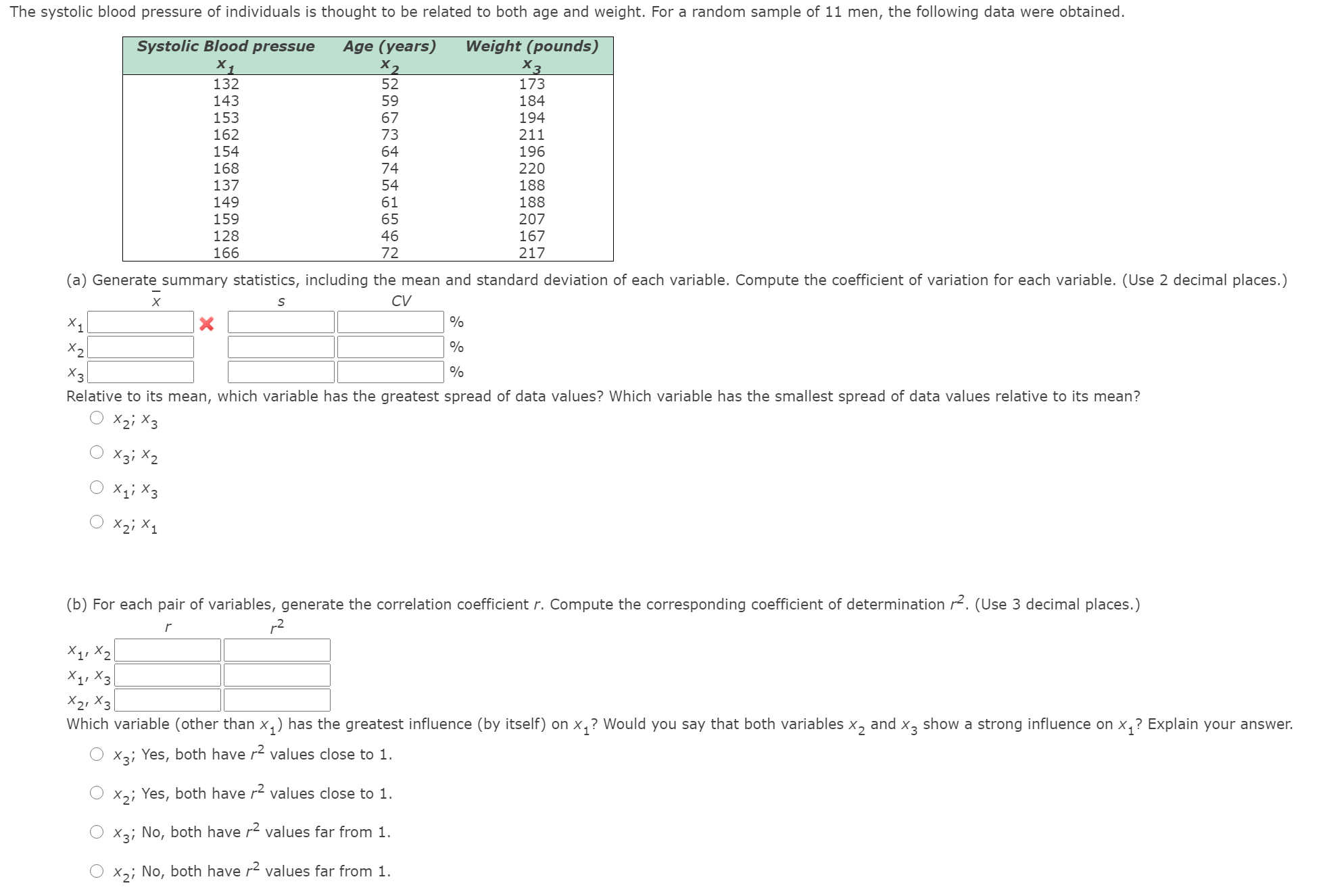
The systolic blood pressure of individuals is thought to be related to both age and weight. For a random sample of 11 men, the following data were obtained. Systolic Blood pressue Age (years) Weight (pounds) X X X 1 2 3 132 52 173 143 59 184 153 67 194 162 73 211 154 64 196 168 74 220 137 54 188 149 61 188 159 65 207 128 46 167 166 72 217 (a) Generatesummary statistics, including the mean and standard deviation of each variable. Compute the coefficient of variation for each variable. (Use 2 decimal places.) x 5 CV xll Ix l H l % le | l ll l % Xsl | l H l \"/o Relative to its mean, which variable has the greatest spread of data values? Which variable has the smallest spread of data values relative to its mean? 0 x2; X 0 x3; x2 0 x1; x3 0 x2; x1 (b) For each pair of variables, generate the correlation coefficient r. Compute the corresponding coefficient of determination r2. (Use 3 decimal places.) r r2 X1. X2:: X1: HE: wag: Which variable (other than x1) has the greatest influence (by itself) on X1? Would you say that both variables X2 and x3 show a strong influence on x1? Explain your answer. 0 x3; Yes, both have r2 values close to 1. 0 x2; Yes, both have r2 values close to 1. 0 x3; No, both have r2 values farfrom l. 0 x2; No, both have r2 values farfrom 1. What percent of the variation in x1 can be explained by the corresponding variation in X2? Answer the same question for X3. (Use 1 decimal place.) x2 % X3 % (c) Perform a regression analysis with x1 as the response variable. Use x2 and x3 as explanatory variables. Look at the coefcient of multiple determination. What percentage of the variation in x1 can be explained by the corresponding variations in X2 and X3 taken together? (Use 1 decimal place.) nla (d) Look at the coefcients of the regression equation. Write out the regression equation. (Use 3 decimal places.) x1 =l:l+:xz+:lx3 Explain how each coefficient can be thought of as a slope. 0 If we look at all coefficients together, each one can be thought of as a "slope." O If we hold all explanatory variables as fixed constants, the intercept can be thought of as a "slope." Q If we look at all coefcients together, the sum of them can be thought of as the overall "slope" of the regression line. Q If we hold all other explanatory variables as xed constants, then we can look at one coefficient as a "slope." If age were held xed, but a person put on 8 pounds, what would you expect for the corresponding change in systolic blood pressure? (Use 2 decimal places.) : If a person kept the same weight but got 8 years older, what would you expect for the corresponding change in systolic blood pressure? (Use 2 decimal places.) : (e) Test each coefcient to determine if it is zero or not zero. Use level of signicance 5%. (Use 2 decimal places for t and 3 decimal places for the P~value.) t P value 1?: 53 Conclusion Q We reject both null hypotheses, there is insufcient evidence that 32 and [3'3 differ from 0. Q We reject both null hypotheses, there is sufcient evidence that [32 and Ba differ from 0. Q We fail to reject both null hypotheses, there is sufcient evidence that [92 and : differ from 0. Q We fail to reject both null hypotheses, there is insufcient evidence that 2 and ,83 differ from O. If age were held fixed, but a person put on 8 pounds, what would you expect for the corresponding change in systolic blood pressure? (Use 2 decimal places.) E If a person kept the same weight but got 8 years older, what would you expect for the corresponding change in systolic blood pressure? (Use 2 decimal places.) S (e) Test each coefficient to determine if it is zero or not zero. Use level of significance 5%. (Use 2 decimal places for t and 3 decimal places for the P-value.) P value 52:: 53:: Conclusion 0 We reject both null hypotheses, there is insufcient evidence that {3'2 and {3'3 differ from 0. 0 We reject both null hypotheses, there is sufficient evidence that {5'2 and [3'3 differ from O. 0 We fail to reject both null hypotheses, there is sufficient evidence that z and g differ from 0. 0 We fail to reject both null hypotheses, there is insufficient evidence that [92 and 3 differ from 0. Why would the outcome of each test help us determine whether or not a given variable should be used in the regression model? 0 If a coefficient is found to be not different from 0, then it contributes to the regression equation. 0 If a coefficient is found to be different from 0, then it does not contribute to the regression equation. 0 If a coefficient is found to be different from 0, then it contributes to the regression equation. 0 If a coefficient is found to be not different from 0, then it does not contribute to the regression equation. (f) Find a 90% confidence interval for each coefficient. (Use 2 decimal places.) lower limit upper limit 52:: 53:: (9) Suppose Michael is 68 years old and weighs 192 pounds. Predict his systolic blood pressure, and find a 90% confidence range for your prediction. (Use 1 decimal place.) warm