Please help with add and remove methods

Implement the AVL class (a subclass of BST) by completing the provided skeleton code in the file avl.py. Once completed, your implementation will include overridden versions of the following methods: add(), remove() And it will inherit the following methods from BST: contains(), inorder_traversal(), find_min(), find_max() is_empty(), make_empty() 2. When reviewing the provided skeleton code, please note that the AVLNode class (a subclass of BSTNode) has two important added attributes: parent (to store a pointer to the parent of the current node) and height (to store the height of the subtree rooted at the current node). Your implementation must correctly maintain all three node pointers (left, right, and parent), as well as the height attribute of each node. Your tree must use the AVLNode class. 3. We will test your implementation with different types of objects, not just integers. We guarantee that all such objects will have correct implementation of methods __eq__(), __lt__(), __gt__(), __ge__(), __le__(), and __str__(). 4. The number of objects stored in the tree will be between 0 and 900 inclusive. 5. When removing a node with two subtrees, replace it with the leftmost child of the right subtree (i.e. the inorder successor). You do not need to recursively continue this process. If the deleted node only has one subtree (either right or left), replace the deleted node with the root node of that subtree. 6. The variables in AVLNode are not private. You are allowed to access and change their values directly. You do not need to write any getter or setter methods for them. The AVL skeleton code includes some suggested helper methods. 7. RESTRICTIONS: You are not allowed to use ANY built-in Python data structures and/or their methods. In case you need helper data structures in your solution, the skeleton code includes prewritten implementations of Queue and Stack classes, which are in separate files and imported in bst.py and avl.py. You are allowed to create and use objects from those classes in your implementation. You are not allowed to directly access any variables of the Queue or Stack classes. All work must be done only by using class methods. 8. Ensure that your methods meet the specified runtime requirements.

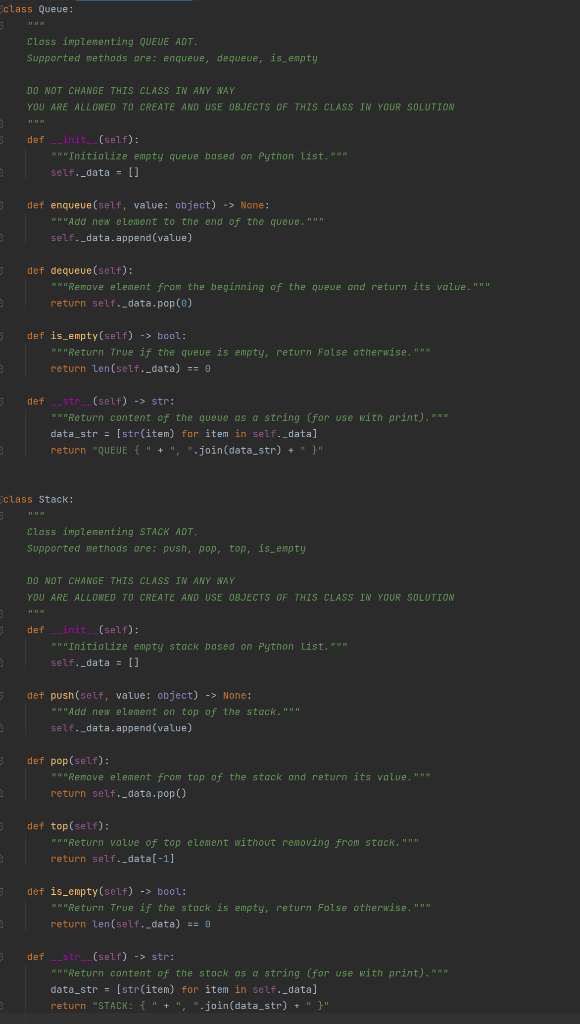
stack and queue

Code requirements

#skeleton code

import random from queue_and_stack import Queue, Stack from bst import BSTNode, BST class AVLNode(BSTNode): """ AVL Tree Node class. Inherits from BSTNode DO NOT CHANGE THIS CLASS IN ANY WAY """ def __init__(self, value: object) -> None: """ Initialize a new AVL node DO NOT CHANGE THIS METHOD IN ANY WAY """ # call __init__() from parent class super().__init__(value) # new variables needed for AVL self.parent = None self.height = 0 def __str__(self) -> str: """ Override string method DO NOT CHANGE THIS METHOD IN ANY WAY """ return 'AVL Node: {}'.format(self.value) class AVL(BST): """ AVL Tree class. Inherits from BST """ def __init__(self, start_tree=None) -> None: """ Initialize a new AVL Tree DO NOT CHANGE THIS METHOD IN ANY WAY """ # call __init__() from parent class super().__init__(start_tree) def __str__(self) -> str: """ Override string method DO NOT CHANGE THIS METHOD IN ANY WAY """ values = [] super()._str_helper(self._root, values) return "AVL pre-order { " + ", ".join(values) + " }" def is_valid_avl(self) -> bool: """ Perform pre-order traversal of the tree. Return False if there are any problems with attributes of any of the nodes in the tree. This is intended to be a troubleshooting 'helper' method to help find any inconsistencies in the tree after the add() or remove() operations. Review the code to understand what this method is checking and how it determines whether the AVL tree is correct. DO NOT CHANGE THIS METHOD IN ANY WAY """ stack = Stack() stack.push(self._root) while not stack.is_empty(): node = stack.pop() if node: # check for correct height (relative to children) left = node.left.height if node.left else -1 right = node.right.height if node.right else -1 if node.height != 1 + max(left, right): return False if node.parent: # parent and child pointers are in sync if node.value  None:

def remove(self, value: object) -> bool:

# ------------------- BASIC TESTING ----------------------------------------- if __name__ == '__main__': print(" PDF - method add() example 1") print("----------------------------") test_cases = ( (1, 2, 3), # RR (3, 2, 1), # LL (1, 3, 2), # RL (3, 1, 2), # LR ) for case in test_cases: tree = AVL(case) print(tree) print(" PDF - method add() example 2") print("----------------------------") test_cases = ( (10, 20, 30, 40, 50), # RR, RR (10, 20, 30, 50, 40), # RR, RL (30, 20, 10, 5, 1), # LL, LL (30, 20, 10, 1, 5), # LL, LR (5, 4, 6, 3, 7, 2, 8), # LL, RR (range(0, 30, 3)), (range(0, 31, 3)), (range(0, 34, 3)), (range(10, -10, -2)), ('A', 'B', 'C', 'D', 'E'), (1, 1, 1, 1), ) for case in test_cases: tree = AVL(case) print('INPUT :', case) print('RESULT :', tree) print(" PDF - method add() example 3") print("----------------------------") for _ in range(100): case = list(set(random.randrange(1, 20000) for _ in range(900))) tree = AVL() for value in case: tree.add(value) if not tree.is_valid_avl(): raise Exception("PROBLEM WITH ADD OPERATION") print('add() stress test finished') print(" PDF - method remove() example 1") print("-------------------------------") test_cases = ( ((1, 2, 3), 1), # no AVL rotation ((1, 2, 3), 2), # no AVL rotation ((1, 2, 3), 3), # no AVL rotation ((50, 40, 60, 30, 70, 20, 80, 45), 0), ((50, 40, 60, 30, 70, 20, 80, 45), 45), # no AVL rotation ((50, 40, 60, 30, 70, 20, 80, 45), 40), # no AVL rotation ((50, 40, 60, 30, 70, 20, 80, 45), 30), # no AVL rotation ) for case, del_value in test_cases: tree = AVL(case) print('INPUT :', tree, "DEL:", del_value) tree.remove(del_value) print('RESULT :', tree) print(" PDF - method remove() example 2") print("-------------------------------") test_cases = ( ((50, 40, 60, 30, 70, 20, 80, 45), 20), # RR ((50, 40, 60, 30, 70, 20, 80, 15), 40), # LL ((50, 40, 60, 30, 70, 20, 80, 35), 20), # RL ((50, 40, 60, 30, 70, 20, 80, 25), 40), # LR ) for case, del_value in test_cases: tree = AVL(case) print('INPUT :', tree, "DEL:", del_value) tree.remove(del_value) print('RESULT :', tree) print(" PDF - method remove() example 3") print("-------------------------------") case = range(-9, 16, 2) tree = AVL(case) for del_value in case: print('INPUT :', tree, del_value) tree.remove(del_value) print('RESULT :', tree) print(" PDF - method remove() example 4") print("-------------------------------") case = range(0, 34, 3) tree = AVL(case) for _ in case[:-2]: root_value = tree.get_root().value print('INPUT :', tree, root_value) tree.remove(root_value) print('RESULT :', tree) print(" PDF - method remove() example 5") print("-------------------------------") for _ in range(100): case = list(set(random.randrange(1, 20000) for _ in range(900))) tree = AVL(case) for value in case[::2]: tree.remove(value) if not tree.is_valid_avl(): raise Exception("PROBLEM WITH REMOVE OPERATION") print('remove() stress test finished') print(" PDF - method contains() example 1") print("---------------------------------") tree = AVL([10, 5, 15]) print(tree.contains(15)) print(tree.contains(-10)) print(tree.contains(15)) print(" PDF - method contains() example 2") print("---------------------------------") tree = AVL() print(tree.contains(0)) print(" PDF - method inorder_traversal() example 1") print("---------------------------------") tree = AVL([10, 20, 5, 15, 17, 7, 12]) print(tree.inorder_traversal()) print(" PDF - method inorder_traversal() example 2") print("---------------------------------") tree = AVL([8, 10, -4, 5, -1]) print(tree.inorder_traversal()) print(" PDF - method find_min() example 1") print("---------------------------------") tree = AVL([10, 20, 5, 15, 17, 7, 12]) print(tree) print("Minimum value is:", tree.find_min()) print(" PDF - method find_min() example 2") print("---------------------------------") tree = AVL([8, 10, -4, 5, -1]) print(tree) print("Minimum value is:", tree.find_min()) print(" PDF - method find_max() example 1") print("---------------------------------") tree = AVL([10, 20, 5, 15, 17, 7, 12]) print(tree) print("Maximum value is:", tree.find_max()) print(" PDF - method find_max() example 2") print("---------------------------------") tree = AVL([8, 10, -4, 5, -1]) print(tree) print("Maximum value is:", tree.find_max()) print(" PDF - method is_empty() example 1") print("---------------------------------") tree = AVL([10, 20, 5, 15, 17, 7, 12]) print("Tree is empty:", tree.is_empty()) print(" PDF - method is_empty() example 2") print("---------------------------------") tree = AVL() print("Tree is empty:", tree.is_empty()) print(" PDF - method make_empty() example 1") print("---------------------------------") tree = AVL([10, 20, 5, 15, 17, 7, 12]) print("Tree before make_empty():", tree) tree.make_empty() print("Tree after make_empty(): ", tree) print(" PDF - method make_empty() example 2") print("---------------------------------") tree = AVL() print("Tree before make_empty():", tree) tree.make_empty() print("Tree after make_empty(): ", tree) 

add(self, value: object) -> None: This method adds a new value to the tree while maintaining its AVL property. Duplicate values are not allowed. If the value is already in the tree, the method should not change the tree. It must be implemented with O(logN) runtime complexity. Example \#1: CS261 Data Structures Assignment 4: BST/AVL Tree Implementation Example \#3: remove(self, value: object) > bool: This method removes the value from the AVL tree. The method returns True if the value is removed. Otherwise, it returns False. It must be implemented with O(logN) runtime complexity. NOTE: See 'Specific Instructions' for an explanation of which node replaces the deleted node. Example \#1: xxmrple A2: Cor case, sat valie in teat caaca: tree - siticagel tree.remove idel_value: frine ('aRsonet :' treai Gustusti. INEOI : WI pro-order : 50, 10,20,40,65,70,60,80, DEL : 20 riten ; Aul pre-prter 450,40,39,45,70,60,601 INEUI : RIL prC-OEdAI: 50,30,20,40,35,70,60,80 I DEL 20 INFOT : AV prc-oEdar: 50,30,20,25,40,70,60,80 I DEL 40 BESUL? : sut pre-oeder {50,25,20,30,70,60,0001 Lable of Cimptents. Pace 21 of 23 Example \#4: case = range (0,34,3) tree = AVL (case) for - in case [:2]: root value = tree.get_root().value print ('INPUT :', tree, root_value) tree.remove (root,value) print ('RESULT :', tree) Output: INPUT : AVL pre-order {21,9,3,0,6,15,12,18,27,24,30,33}21 RESULT : AVL pre-order {24,9,3,0,6,15,12,18,30,27,33} INPUT : AVL pre-order {24,9,3,0,6,15,12,18,30,27,33}24 RESULT : AVL pre-order {27,9,3,0,6,15,12,18,30,33} INPUT : AVL pre-order {27,9,3,0,6,15,12,18,30,33}27 RESULT : AVL pre-order {9,3,0,6,30,15,12,18,33} INPUT : AVL pre-order {9,3,0,6,30,15,12,18,33}9 RESULT : AVL pre-order {12,3,0,6,30,15,18,33} INPUT : AVL pre-order {12,3,0,6,30,15,18,33}12 RESULT : AVL pre-order {15,3,0,6,30,18,33} INPUT : AVL pre-order {15,3,0,6,30,18,33}15 RESULT : AVL pre-order {18,3,0,6,30,33} INPUT : AVL pre-order {18,3,0,6,30,33}18 RESULT : AVL pre-order {30,3,0,6,33} INPUT : AVL pre-order {30,3,0,6,33}30 RESULT : AVL pre-order {3,0,33,6} INPUT : AVL pre-order {3,0,33,6}3 RESULT : AVL pre-order {6,0,33} INPUT : AVL pre-order {6,0,33}6 RESULT : AVL pre-order {33,0} Example \#5: for - in range (100) : case = list ( set ( random.randrange (1,20000) for in range(900)) ) tree =AVL (case) for value in case [::2] : tree.remove (value) if not tree.is_valid_avl () : raise Exception ("PROBLEM WITH REMOVE OPERATION") print('Stress test finished') gutput: remove() stress test finished add(self, value: object) -> None: This method adds a new value to the tree while maintaining its AVL property. Duplicate values are not allowed. If the value is already in the tree, the method should not change the tree. It must be implemented with O(logN) runtime complexity. Example \#1: CS261 Data Structures Assignment 4: BST/AVL Tree Implementation Example \#3: remove(self, value: object) > bool: This method removes the value from the AVL tree. The method returns True if the value is removed. Otherwise, it returns False. It must be implemented with O(logN) runtime complexity. NOTE: See 'Specific Instructions' for an explanation of which node replaces the deleted node. Example \#1: xxmrple A2: Cor case, sat valie in teat caaca: tree - siticagel tree.remove idel_value: frine ('aRsonet :' treai Gustusti. INEOI : WI pro-order : 50, 10,20,40,65,70,60,80, DEL : 20 riten ; Aul pre-prter 450,40,39,45,70,60,601 INEUI : RIL prC-OEdAI: 50,30,20,40,35,70,60,80 I DEL 20 INFOT : AV prc-oEdar: 50,30,20,25,40,70,60,80 I DEL 40 BESUL? : sut pre-oeder {50,25,20,30,70,60,0001 Lable of Cimptents. Pace 21 of 23 Example \#4: case = range (0,34,3) tree = AVL (case) for - in case [:2]: root value = tree.get_root().value print ('INPUT :', tree, root_value) tree.remove (root,value) print ('RESULT :', tree) Output: INPUT : AVL pre-order {21,9,3,0,6,15,12,18,27,24,30,33}21 RESULT : AVL pre-order {24,9,3,0,6,15,12,18,30,27,33} INPUT : AVL pre-order {24,9,3,0,6,15,12,18,30,27,33}24 RESULT : AVL pre-order {27,9,3,0,6,15,12,18,30,33} INPUT : AVL pre-order {27,9,3,0,6,15,12,18,30,33}27 RESULT : AVL pre-order {9,3,0,6,30,15,12,18,33} INPUT : AVL pre-order {9,3,0,6,30,15,12,18,33}9 RESULT : AVL pre-order {12,3,0,6,30,15,18,33} INPUT : AVL pre-order {12,3,0,6,30,15,18,33}12 RESULT : AVL pre-order {15,3,0,6,30,18,33} INPUT : AVL pre-order {15,3,0,6,30,18,33}15 RESULT : AVL pre-order {18,3,0,6,30,33} INPUT : AVL pre-order {18,3,0,6,30,33}18 RESULT : AVL pre-order {30,3,0,6,33} INPUT : AVL pre-order {30,3,0,6,33}30 RESULT : AVL pre-order {3,0,33,6} INPUT : AVL pre-order {3,0,33,6}3 RESULT : AVL pre-order {6,0,33} INPUT : AVL pre-order {6,0,33}6 RESULT : AVL pre-order {33,0} Example \#5: for - in range (100) : case = list ( set ( random.randrange (1,20000) for in range(900)) ) tree =AVL (case) for value in case [::2] : tree.remove (value) if not tree.is_valid_avl () : raise Exception ("PROBLEM WITH REMOVE OPERATION") print('Stress test finished') gutput: remove() stress test finished