Please help with this code. I've attached and example of how to start the problem to have an idea.

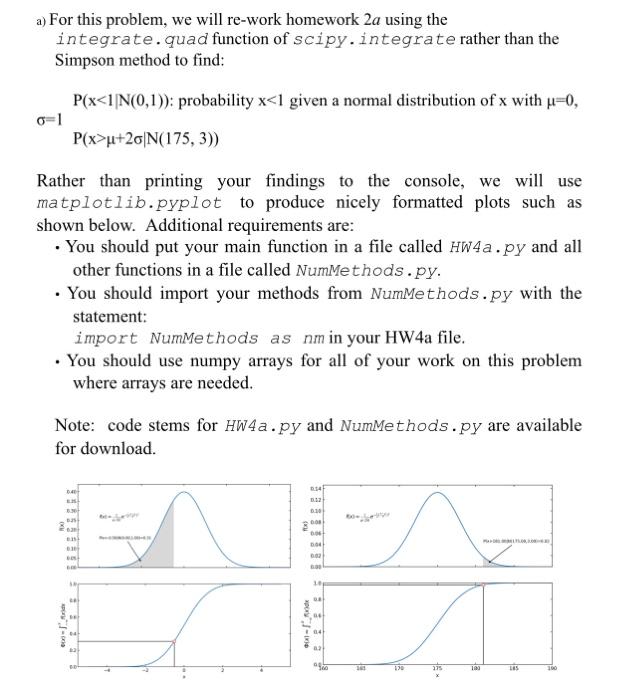
a) For this problem, we will re-work homework 2a using the integrate.quad function of scipy.integrate rather than the Simpson method to find: P(xu+26|N(175, 3)) Rather than printing your findings to the console, we will use matplotlib.pyplot to produce nicely formatted plots such as shown below. Additional requirements are: . You should put your main function in a file called HW4a.py and all other functions in a file called NumMethods.py. . You should import your methods from NumMethods.py with the statement: import NumMethods as nm in your HW4a file. . You should use numpy arrays for all of your work on this problem where arrays are needed. Note: code stems for HW4a.py and Nummethods.py are available for download. 0.4 1 120 100 LES import matplotlib.pyplot as plt import NumMethods as nm import numpy as np def main(): Calculates P(x}+2f |N(175, 3)) and displays both the GNPDF and CDF for each case :return: #part 1. P(x, connectionstyle="arc3")) #draw the arrow with text plt.ylabel('f(x), size=12) #add a label to the y axis ax.tick_params (axis='both', which='both', direction='in', top=True, right=True, labelsize=10) # format tick marks ax.xaxis.set_ticklabels(1) #erase x tick labels for the top graph #create the CDF plot plt.subplot(2,1,2) #select the second plot plt.plot (#&MISSING CODE HERE) #plot cdf_a vs X_a plt.ylim(0,1) #set limits for the y axis plt.ylabel(#&MISSING CODE HERE, size=12) #label the y axis plt.xlabel('x') #add the x label plt.plot (#&MISSING CODE HERE, 'o', markerfacecolor='white', markeredgecolor='red') #put a red circle on the cdf at location c_a, p_a ax=plt.gca() #get the current set of axes ax.tick_params (axis='both', which='both', direction='in', top=True, right=True, labelsize=10) # format tick marks ax.set_xlim(x_a.min(), x_a.max()) #make sure the x axis has the correct limits ax.hlines (p_a, ax.get_xlim()[0],c_a, color='black', linewidth=1) #draw a horizontal line connecting the y axis to the red circle ax.vlines (c_a, 0, p_a, color='black', linewidth=1) #draw a vertical line connecting the x axis to the red circle plt.show() #show the plot. Note, the code stops here and waits for the user to close the figure window #part 2. P(xu+20|N(175, 3)) Print you findings to the console in the following format: P(x181.00 N(175,3))=Z.ZZ a) For this problem, we will re-work homework 2a using the integrate.quad function of scipy.integrate rather than the Simpson method to find: P(xu+26|N(175, 3)) Rather than printing your findings to the console, we will use matplotlib.pyplot to produce nicely formatted plots such as shown below. Additional requirements are: . You should put your main function in a file called HW4a.py and all other functions in a file called NumMethods.py. . You should import your methods from NumMethods.py with the statement: import NumMethods as nm in your HW4a file. . You should use numpy arrays for all of your work on this problem where arrays are needed. Note: code stems for HW4a.py and Nummethods.py are available for download. 0.4 1 120 100 LES import matplotlib.pyplot as plt import NumMethods as nm import numpy as np def main(): Calculates P(x}+2f |N(175, 3)) and displays both the GNPDF and CDF for each case :return: #part 1. P(x, connectionstyle="arc3")) #draw the arrow with text plt.ylabel('f(x), size=12) #add a label to the y axis ax.tick_params (axis='both', which='both', direction='in', top=True, right=True, labelsize=10) # format tick marks ax.xaxis.set_ticklabels(1) #erase x tick labels for the top graph #create the CDF plot plt.subplot(2,1,2) #select the second plot plt.plot (#&MISSING CODE HERE) #plot cdf_a vs X_a plt.ylim(0,1) #set limits for the y axis plt.ylabel(#&MISSING CODE HERE, size=12) #label the y axis plt.xlabel('x') #add the x label plt.plot (#&MISSING CODE HERE, 'o', markerfacecolor='white', markeredgecolor='red') #put a red circle on the cdf at location c_a, p_a ax=plt.gca() #get the current set of axes ax.tick_params (axis='both', which='both', direction='in', top=True, right=True, labelsize=10) # format tick marks ax.set_xlim(x_a.min(), x_a.max()) #make sure the x axis has the correct limits ax.hlines (p_a, ax.get_xlim()[0],c_a, color='black', linewidth=1) #draw a horizontal line connecting the y axis to the red circle ax.vlines (c_a, 0, p_a, color='black', linewidth=1) #draw a vertical line connecting the x axis to the red circle plt.show() #show the plot. Note, the code stops here and waits for the user to close the figure window #part 2. P(xu+20|N(175, 3)) Print you findings to the console in the following format: P(x181.00 N(175,3))=Z.ZZ