please i do need help with this questions.
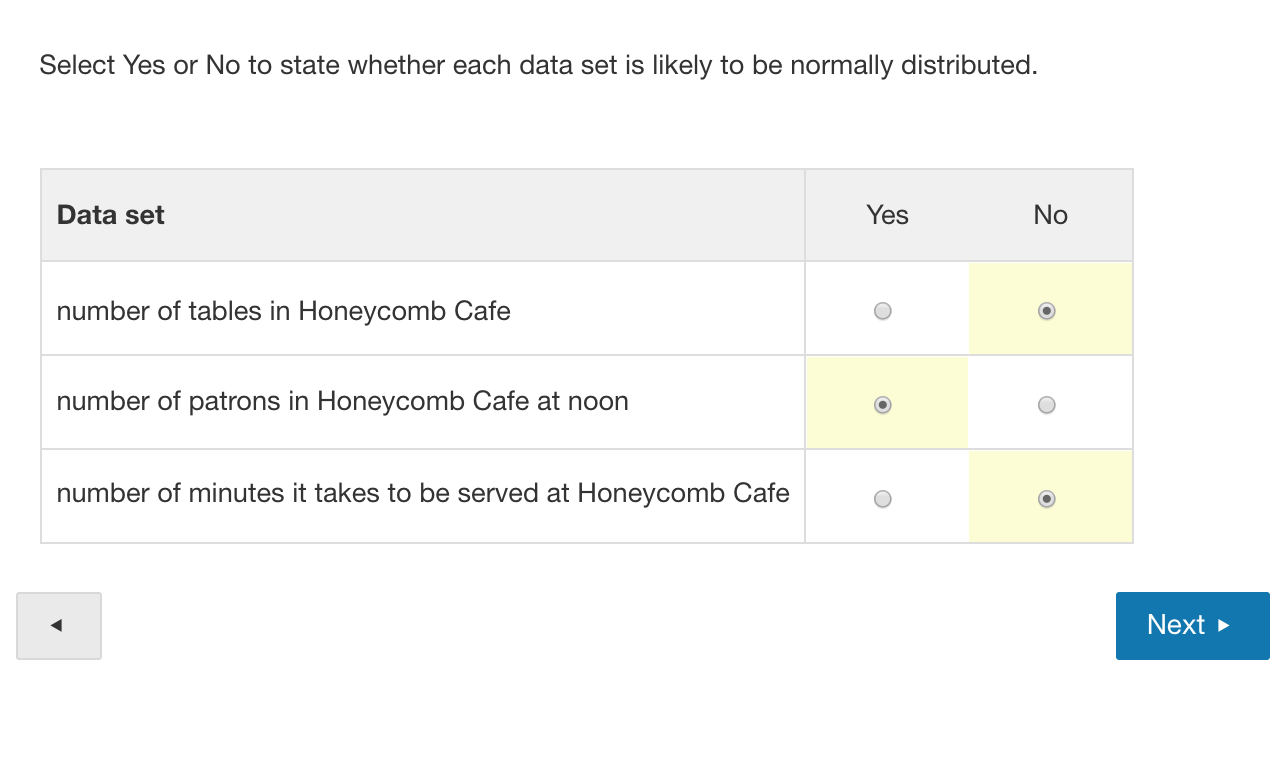
A new drug claims to reduce the number of eczema breakouts an individual suffers. In a study on the effectiveness of the new drug, 50 subjects were given the new drug and another 50 subjects were given a placebo. At the end of the 6month study, the group given the new drug reported an average of 1.3 breakouts a month. The group given the placebo reported an average of 4.5 breakouts a month. The data from the study are rerandomized 10 times. The difference of the means from rerandomization are 1.5, 3.0, 1.8, 1.3, 2.1, 1.9, 2.5, 0.7, 2.1 , and 1.9. What is the most appropriate conclusion about the new drug to draw from this information? The new drug does not appear to reduce the number of eczema breakouts since the O rerandomized mean differences are considerably greater than the mean difference found between the two groups studied. The new drug does not appear to reduce the number of eczema breakouts since the O rerandomized mean differences are close to the mean difference found between the two groups studied. The new drug appears to reduce the number of eczema breakouts since the O rerandomized mean differences are considerably less than the mean difference found between the two groups studied. The new drug appears to reduce the number of eczema breakouts since the O rerandomized mean differences are close to the mean difference found between the two groups studied. Martin is offered 2 options on how to move his token in a board game. The objective of the game is to move forward to the finish line. The spinner used in the game has 4 equally sized sectors labeled 1, 3, 4, and 6. OPTION A: Spin the spinner twice. If the sum of the spins is greater than 8, move token forward 4 spaces. Else, move token back 1 space. OPTION B: Spin the spinner once. If the spin is a prime number, move token forward 8 spaces. Else, move token back 2 spaces. Which description offers the correct analysis of the choice Martin should make to have the greatest likelihood of winning the game? Martin should choose Option A. The mathematical expectation of Option A is 0.5625 and the mathematical expectation of Option B is 3. Martin should choose Option A. The mathematical expectation of Option A is 0.5625 and the mathematical expectation of Option B is 0.5. Martin should choose Option B. The mathematical expectation of Option A is 0.5625 and the mathematical expectation of Option B is 0.5. Martin should choose Option B. The mathematical expectation of Option A is 0.5625 and the mathematical expectation of Option B is 3. Abe is a game show contestant and is offered a choice. He may accept $500 cash or take a chance at playing a game where he could win $10,000. The game consists of drawing two slips of paper from a hat, without replacement. The hat contains 10 slips of paper numbered with consecutive multiples of 5, beginning with 5 and ending with 50. If both slips of paper selected are less than 20, Abe wins $10,000. If Abe opts to play the game and loses, he does not receive any money at all. Which statement correctly explains the choice Abe should make to win the most money? Abe should accept the $500 and not play the game. The mathematical expectation of the game is $1333.33. Abe should accept the $500 and not play the game. The mathematical expectation of the game is $666.67. Abe should not accept the $500 and play the game. The mathematical expectation of the game is $666.67. Abe should not accept the $500 and play the game. The mathematical expectation of the game is $1333.33. Select Yes or No to state whether each data set is likely to be normally distributed. Data set Yes No number of tables in Honeycomb Cafe 0 number of patrons in Honeycomb Cafe at noon (9 0 number of minutes it takes to be served at Honeycomb Cafe 0 (9 A randomized study compared two drugs that are designed to lower a person's serotonin level. It was found that over a 1-year period, those receiving Drug A decreased their serotonin level by a mean of 36 nanograms per millimeter. Those receiving Drug B decreased their serotonin level by a mean of 20 nanograms per millimeter. To determine whether the results are significant, the data are rerandomized and the difference of the means is shown in the dot plot. What is the best conclusion to make based on the data? The difference of the means is not significant because the O rerandomizations show that it is outside the range of what likely happens by chance. The difference of the means is significant because the @ rerandomizations show that it is outside the range of what likely happens by chance. The difference of the means is not significant because the O rerandomizations show that it is within the range of what likely happens by chance. The difference of the means is significant because the O rerandomizations show that it is within the range of what likely happens by chance. Difference of Ileana I I I I I I I llllllllllI 4 6 1D 12 14 16 1820222426 Ajar contains black marbles and green marbles. Sixty percent of the marbles in the jar are green. A number generator simulates randomly selecting 10 marbles from the jar. The number generator is used 12 times and the number of green marbles in each trial is shown in the dot plot. Which description is correct about the number generator being fair or not? The number generator is fair. The O dot plot shows a distribution that is skewed right. The number generator is fair. It 0 shows that 60% of the marbles selected are green most of the time. The number generator is not fair. 0 The dot plot shows 80% of the marbles drawn are green. The number generator is not fair. In most of the experiments, considerably less than 60% of the selected marbles are green. Random Number Generator Results I re (A! .5 01 an an on re