Question
Please implement a single mapreduce on PySpark to compute a matrix multiplication, i.e., Cnxn = Anxn X Bnxn. Here I provide you the pseudocode and
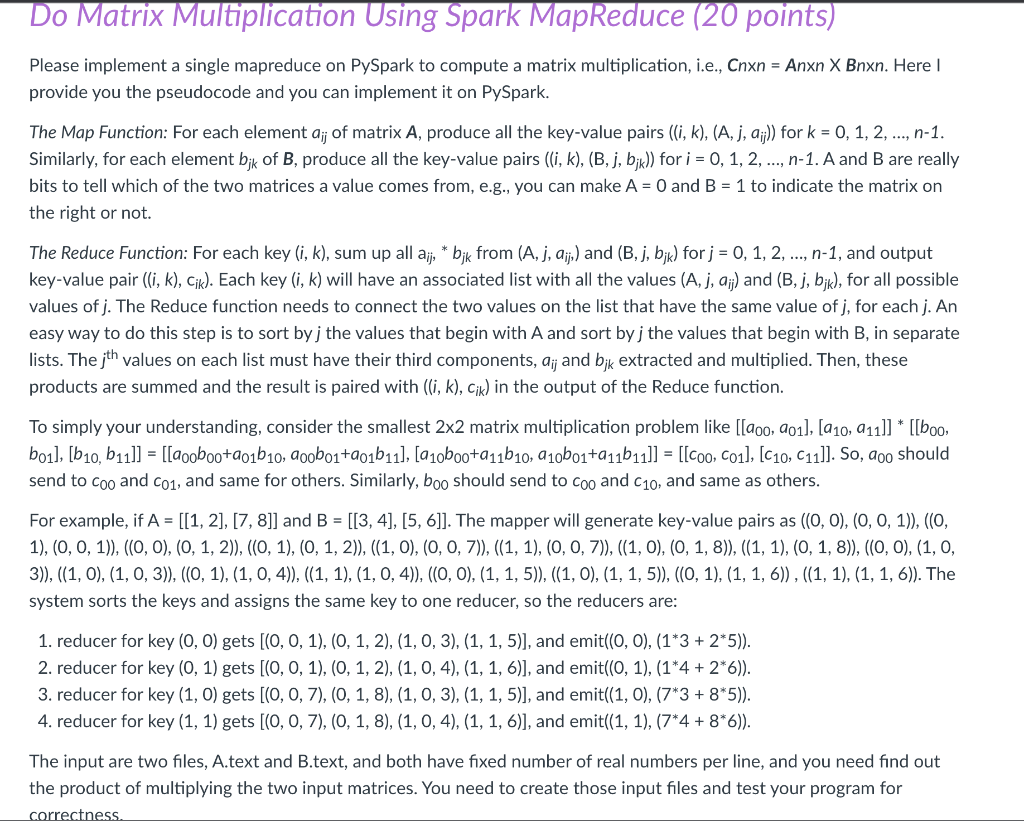 Please implement a single mapreduce on PySpark to compute a matrix multiplication, i.e., Cnxn = Anxn X Bnxn. Here I provide you the pseudocode and you can implement it on PySpark. The Map Function: For each element aij of matrix A, produce all the key-value pairs ((i, k), (A, j, aij)) for k = 0, 1, 2, , n-1. Similarly, for each element bjk of B, produce all the key-value pairs ((i, k), (B, j, bjk)) for i = 0, 1, 2, , n-1. A and B are really bits to tell which of the two matrices a value comes from, e.g., you can make A = 0 and B = 1 to indicate the matrix on the right or not. The Reduce Function: For each key (i, k), sum up all aij, * bjk from (A, j, aij,) and (B, j, bjk) for j = 0, 1, 2, , n-1, and output key-value pair ((i, k), cik). Each key (i, k) will have an associated list with all the values (A, j, aij) and (B, j, bjk), for all possible values of j. The Reduce function needs to connect the two values on the list that have the same value of j, for each j. An easy way to do this step is to sort by j the values that begin with A and sort by j the values that begin with B, in separate lists. The jth values on each list must have their third components, aij and bjk extracted and multiplied. Then, these products are summed and the result is paired with ((i, k), cik) in the output of the Reduce function. To simply your understanding, consider the smallest 2x2 matrix multiplication problem like [[a00, a01], [a10, a11]] * [[b00, b01], [b10, b11]] = [[a00b00+a01b10, a00b01+a01b11], [a10b00+a11b10, a10b01+a11b11]] = [[c00, c01], [c10, c11]]. So, a00 should send to c00 and c01, and same for others. Similarly, b00 should send to c00 and c10, and same as others. For example, if A = [[1, 2], [7, 8]] and B = [[3, 4], [5, 6]]. The mapper will generate key-value pairs as ((0, 0), (0, 0, 1)), ((0, 1), (0, 0, 1)), ((0, 0), (0, 1, 2)), ((0, 1), (0, 1, 2)), ((1, 0), (0, 0, 7)), ((1, 1), (0, 0, 7)), ((1, 0), (0, 1, 8)), ((1, 1), (0, 1, 8)), ((0, 0), (1, 0, 3)), ((1, 0), (1, 0, 3)), ((0, 1), (1, 0, 4)), ((1, 1), (1, 0, 4)), ((0, 0), (1, 1, 5)), ((1, 0), (1, 1, 5)), ((0, 1), (1, 1, 6)) , ((1, 1), (1, 1, 6)). The system sorts the keys and assigns the same key to one reducer, so the reducers are: reducer for key (0, 0) gets [(0, 0, 1), (0, 1, 2), (1, 0, 3), (1, 1, 5)], and emit((0, 0), (1*3 + 2*5)). reducer for key (0, 1) gets [(0, 0, 1), (0, 1, 2), (1, 0, 4), (1, 1, 6)], and emit((0, 1), (1*4 + 2*6)). reducer for key (1, 0) gets [(0, 0, 7), (0, 1, 8), (1, 0, 3), (1, 1, 5)], and emit((1, 0), (7*3 + 8*5)). reducer for key (1, 1) gets [(0, 0, 7), (0, 1, 8), (1, 0, 4), (1, 1, 6)], and emit((1, 1), (7*4 + 8*6)). The input are two files, A.text and B.text, and both have fixed number of real numbers per line, and you need find out the product of multiplying the two input matrices. You need to create those input files and test your program for correctness.
Please implement a single mapreduce on PySpark to compute a matrix multiplication, i.e., Cnxn = Anxn X Bnxn. Here I provide you the pseudocode and you can implement it on PySpark. The Map Function: For each element aij of matrix A, produce all the key-value pairs ((i, k), (A, j, aij)) for k = 0, 1, 2, , n-1. Similarly, for each element bjk of B, produce all the key-value pairs ((i, k), (B, j, bjk)) for i = 0, 1, 2, , n-1. A and B are really bits to tell which of the two matrices a value comes from, e.g., you can make A = 0 and B = 1 to indicate the matrix on the right or not. The Reduce Function: For each key (i, k), sum up all aij, * bjk from (A, j, aij,) and (B, j, bjk) for j = 0, 1, 2, , n-1, and output key-value pair ((i, k), cik). Each key (i, k) will have an associated list with all the values (A, j, aij) and (B, j, bjk), for all possible values of j. The Reduce function needs to connect the two values on the list that have the same value of j, for each j. An easy way to do this step is to sort by j the values that begin with A and sort by j the values that begin with B, in separate lists. The jth values on each list must have their third components, aij and bjk extracted and multiplied. Then, these products are summed and the result is paired with ((i, k), cik) in the output of the Reduce function. To simply your understanding, consider the smallest 2x2 matrix multiplication problem like [[a00, a01], [a10, a11]] * [[b00, b01], [b10, b11]] = [[a00b00+a01b10, a00b01+a01b11], [a10b00+a11b10, a10b01+a11b11]] = [[c00, c01], [c10, c11]]. So, a00 should send to c00 and c01, and same for others. Similarly, b00 should send to c00 and c10, and same as others. For example, if A = [[1, 2], [7, 8]] and B = [[3, 4], [5, 6]]. The mapper will generate key-value pairs as ((0, 0), (0, 0, 1)), ((0, 1), (0, 0, 1)), ((0, 0), (0, 1, 2)), ((0, 1), (0, 1, 2)), ((1, 0), (0, 0, 7)), ((1, 1), (0, 0, 7)), ((1, 0), (0, 1, 8)), ((1, 1), (0, 1, 8)), ((0, 0), (1, 0, 3)), ((1, 0), (1, 0, 3)), ((0, 1), (1, 0, 4)), ((1, 1), (1, 0, 4)), ((0, 0), (1, 1, 5)), ((1, 0), (1, 1, 5)), ((0, 1), (1, 1, 6)) , ((1, 1), (1, 1, 6)). The system sorts the keys and assigns the same key to one reducer, so the reducers are: reducer for key (0, 0) gets [(0, 0, 1), (0, 1, 2), (1, 0, 3), (1, 1, 5)], and emit((0, 0), (1*3 + 2*5)). reducer for key (0, 1) gets [(0, 0, 1), (0, 1, 2), (1, 0, 4), (1, 1, 6)], and emit((0, 1), (1*4 + 2*6)). reducer for key (1, 0) gets [(0, 0, 7), (0, 1, 8), (1, 0, 3), (1, 1, 5)], and emit((1, 0), (7*3 + 8*5)). reducer for key (1, 1) gets [(0, 0, 7), (0, 1, 8), (1, 0, 4), (1, 1, 6)], and emit((1, 1), (7*4 + 8*6)). The input are two files, A.text and B.text, and both have fixed number of real numbers per line, and you need find out the product of multiplying the two input matrices. You need to create those input files and test your program for correctness.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


