please just let me know the answers. i do not need any explaination.
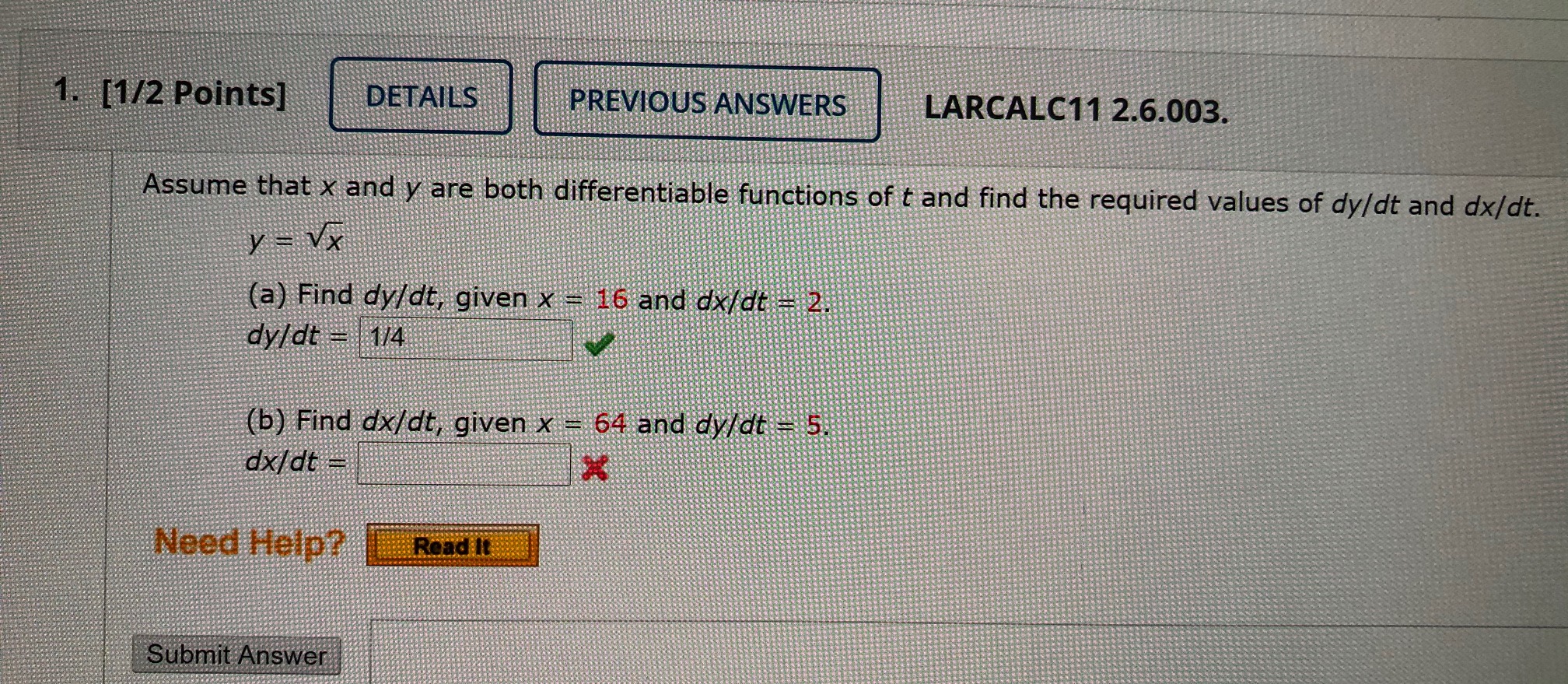
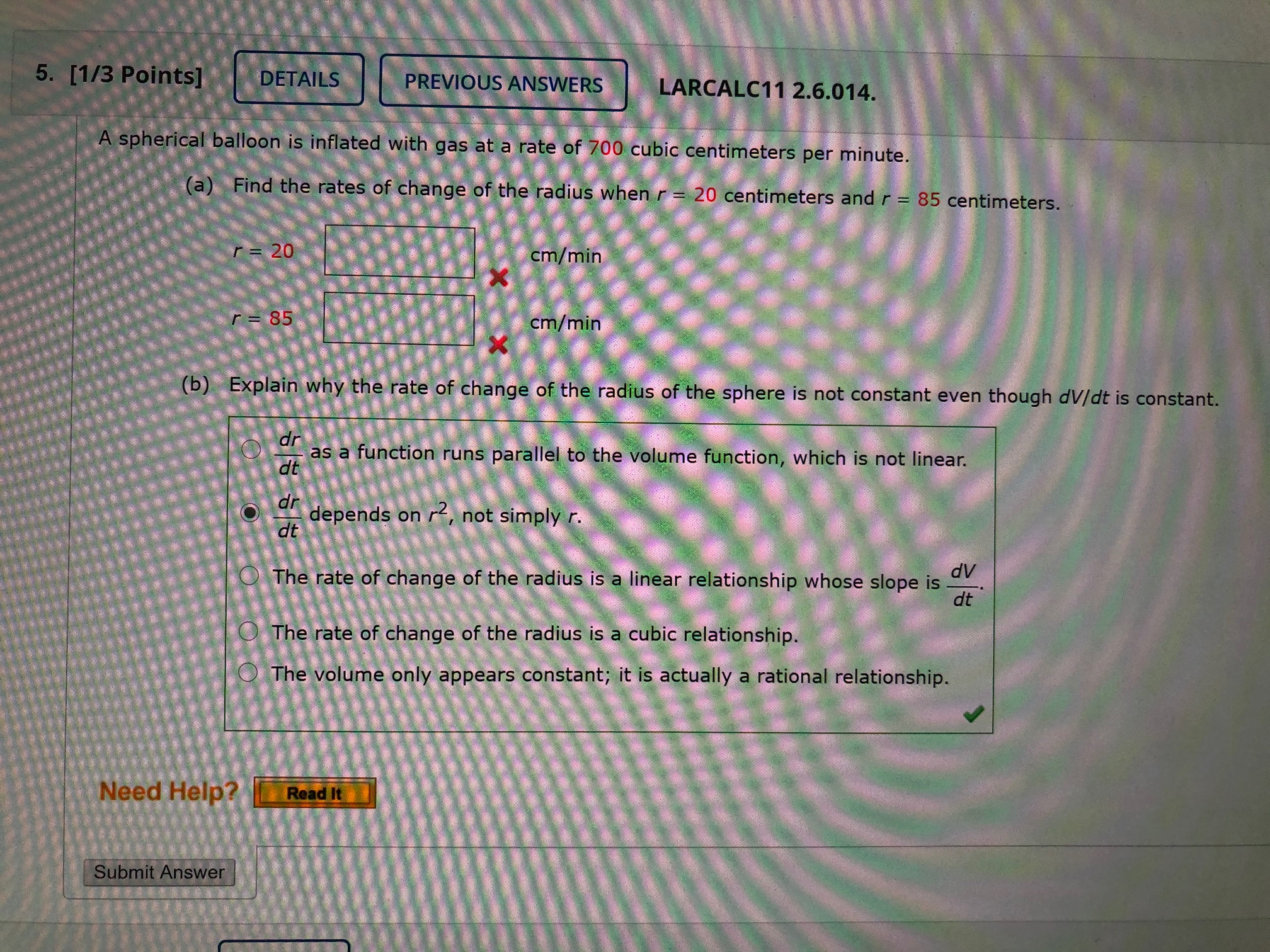
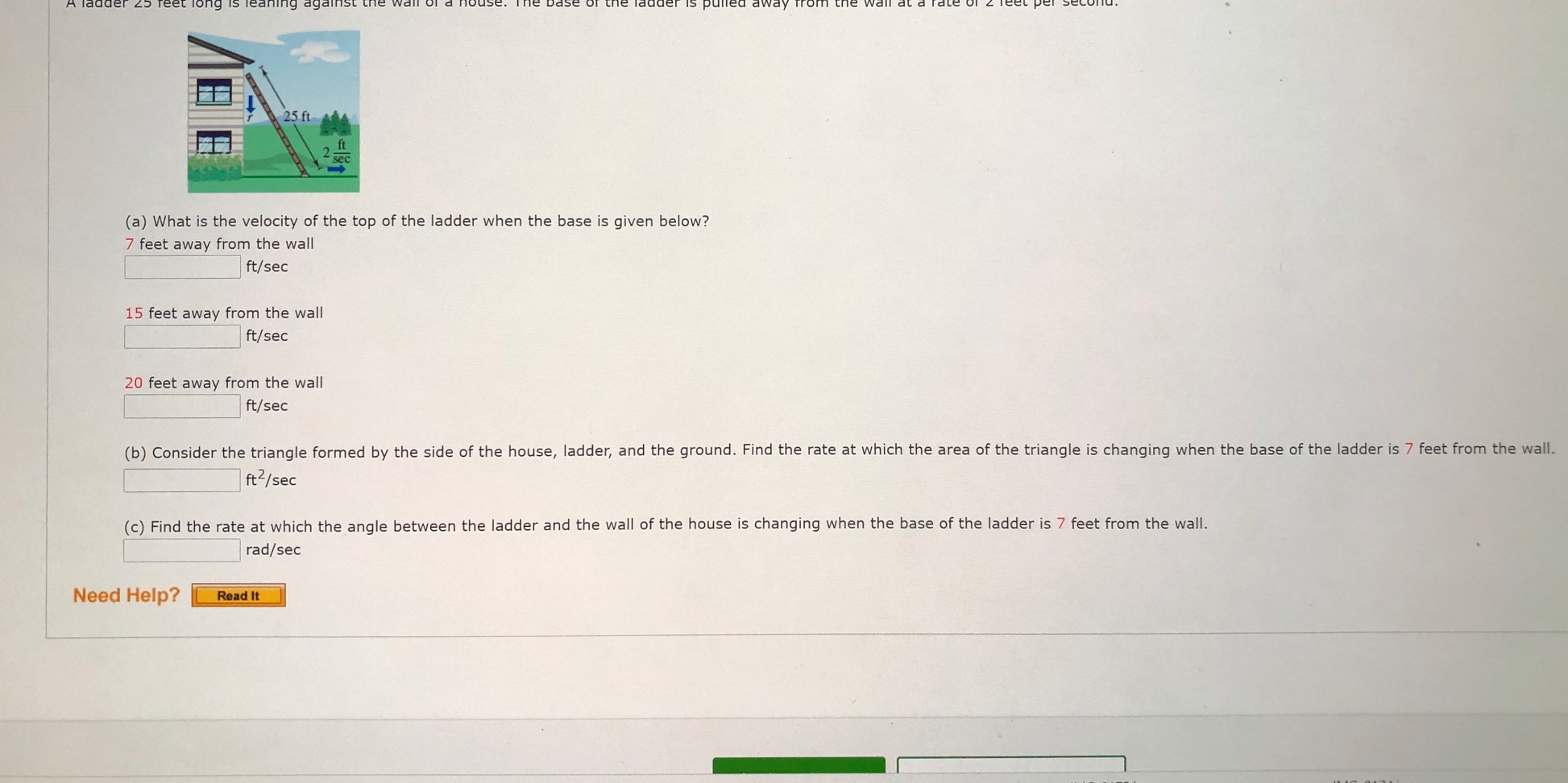
1. [1/2 Points] DETAILS PREVIOUS ANSWERS LARCALC11 2.6.003. Assume that x and y are both differentiable functions of t and find the required values of dy/dt and dx/dt. y - Vx (a) Find dy/dt, given x = 16 and dx/dt = 2. dy/dt = 1/4 (b) Find dx/dt, given x = 64 and dy/dt = 5 dx/ dt = Need Help? Read It Submit Answer5. [1/3 Points] DETAILS PREVIOUS ANSWERS LARCALC11 2.6.014. A spherical balloon is inflated with gas at a rate of 700 cubic centimeters per minute. (a) Find the rates of change of the radius when r = 20 centimeters and r = 85 centimeters. cm/min 85 cm/min (b) Explain why the rate of change of the radius of the sphere is not constant even though dV/dt is constant. dra dt as a function runs parallel to the volume function, which is not linear. depends on r2, not simply r. dt The rate of change of the radius is a linear relationship whose slope is - dv dt The rate of change of the radius is a cubic relationship. The volume only appears constant; it is actually a rational relationship. Need Help? Read It Submit Answer6. [-/1 Points] DETAILS LARCALC11 2.6.017.MI. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHE At a sand and gravel plant, sand is falling off a conveyor and onto a conical pile at a rate of 16 cubic feet per minute. The diameter of the base of the cone is approximately three times the altitude. At what rate is the height of the pile changing when the pile is 22 feet high? (Hint: The formula for the volume of a cone is V = mr2h.) h' it/min Need Help? Read It Watch It Master It8. [-/2 Points] DETAILS LARCALC11 2.6.020. A trough is 12 feet long and 3 feet across the top (see figure). Its ends are isosceles triangles with altitudes of 3 feet. 2 ft3 min 12 ft- 3 ft 3 ft th ft (a) If water is being pumped into the trough at 2 cubic feet per minute, how fast is the water level rising when h is 1.0 feet deep? ft/min (b) If the water is rising at a rate of 3/8 inch per minute when h = 2.0, determine the rate at which water is being pumped into the trough. fts/min Need Help? Read It25 ft it L sec (a) What is the velocity of the top of the ladder when the base is given below? 7 feet away from the wall ft/sec 15 feet away from the wall ft/sec 20 feet away from the wall ft/sec (b) Consider the triangle formed by the side of the house, ladder, and the ground. Find the rate at which the area of the triangle is changing when the base of the ladder is 7 feet from the wall. ft 2/ sec (c) Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 7 feet from the wall. rad/sec Need Help? Read It