Please. Python is better.

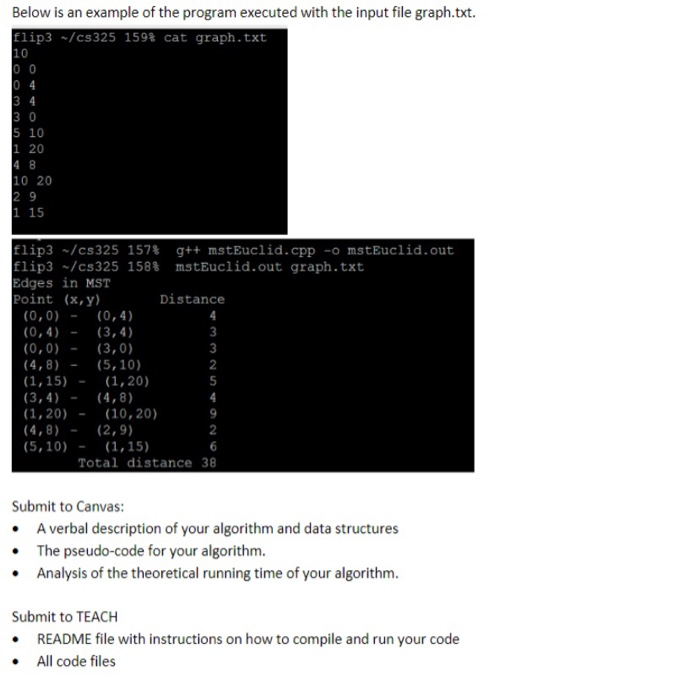
Problem 4: (15 points Euclidean MST Implementation Implement an algorithm in the language of your choice (C, C++ or Python) that determines the MST in a graph G=(VE) where the vertices are points (x,y) in the rectangular coordinate system and the weight of the edge between each pair of points is the Euclidean distance between those points. To avoid floating point precision problems in computing the square-root, we will always round the distance to the nearest integer. For all u, ve V, u = 61.), v = (x,y) and W(u, v) = d(u, v) = nearestint(x1 - x2) + (y1 - y2)? For example, if u = (0,0), v = (1, 3). d(u, v) = nearestint (0 - 1)2 + (0 - 3)2) = nearestint((-1)2 + (-3)2) = nearestint(V1 +9) = nearestint(110) = nearestint(3.1622...) = 3 Assume that the graph G=(V.E) is complete so that there is an edge between every two vertices. Your program (mstEuclid) should read information about the graph from a file given in the command line. Each input file contains information about one graph: the first line in the file is the number of vertices in the graph in s 100) and the following lines contain the x,y coordinates of the vertices in the graph. The output should be displayed to the terminal and contain the edges (x1,72) to (x2,y2) in the MST along with the edge distances and the total distance of the MST. Below is an example of graph4.txt which contains four points (0,0), (0,4), (3,4) and (3,0). The MST has a total distance of 10. (0.4) (3.4) flip3 -/cs325 165% cat graph4.txt 0 0 04 3 4 30 (0:0) (3.0) flip3 -/c3325 166% g++ mstEuclid.cpp -o mstEuclid.out flip3 -/cs325 167% mstEuclid.out graph4.txt Edges in MST Point (x,y) Distance (0,0) - (0,4) (0,4) - (3,4) (0,0) - (3,0) Total distance 10 Below is an example of the program executed with the input file graph.txt. Elip3 -/c5325 1592 cat graph.txt 10 OO 04 30 5 10 1 20 10 20 29 1 15 flip3 -/cs325 1573 g++ mstEuclid.cpp -o mstEuclid.out flip3 -/c3325 158% mstEuclid.out graph.txt Edges in MST Point (x, y) Distance (0,0) - (0,4) (0,4) - (3,4) (0,0) = (3,0) (4,8) - (5,10) (1,15) - (1,20) (3,4) - (4,8) (1,20) - (10,20) (4,8) - (2,9) (5, 10) - (1,15) Total distance 38 Submit to Canvas: A verbal description of your algorithm and data structures The pseudo-code for your algorithm. Analysis of the theoretical running time of your algorithm. Submit to TEACH README file with instructions on how to compile and run your code All code files graph.txt - - px (E) ) W HD 10 100 440 510 120 48 10 20 29 115