Please see attached

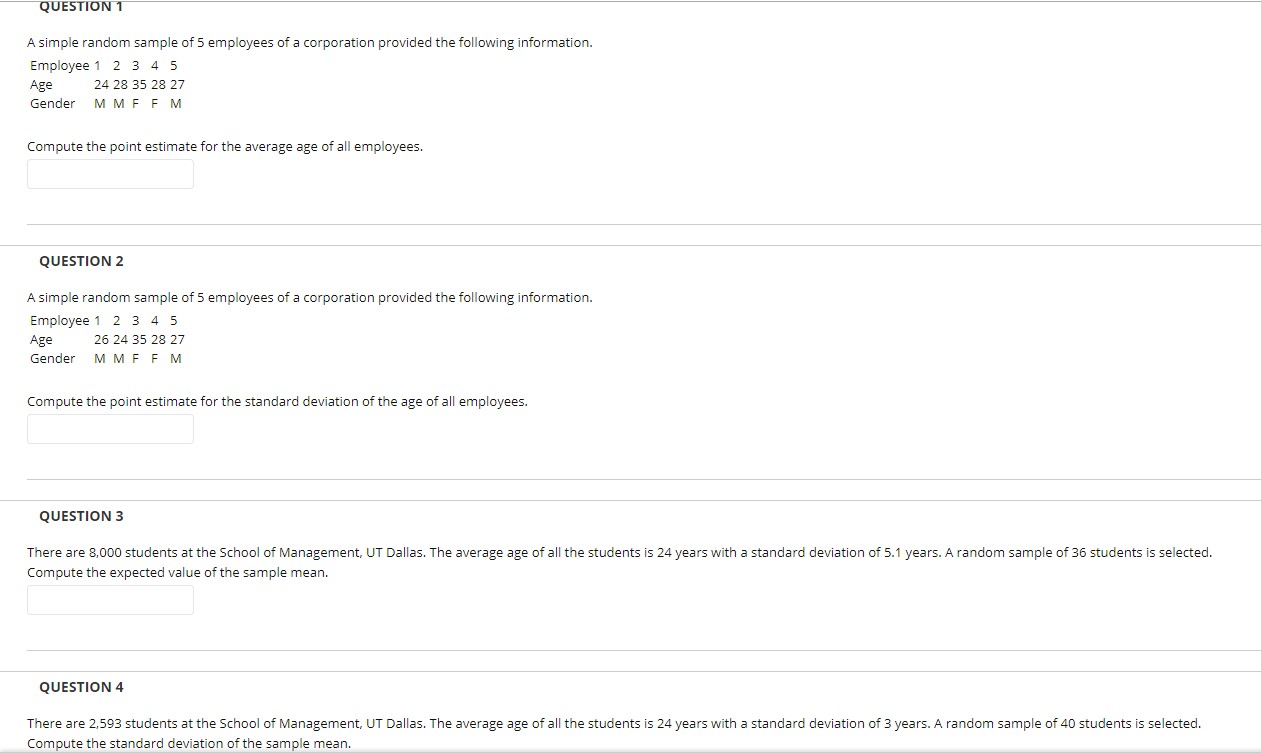
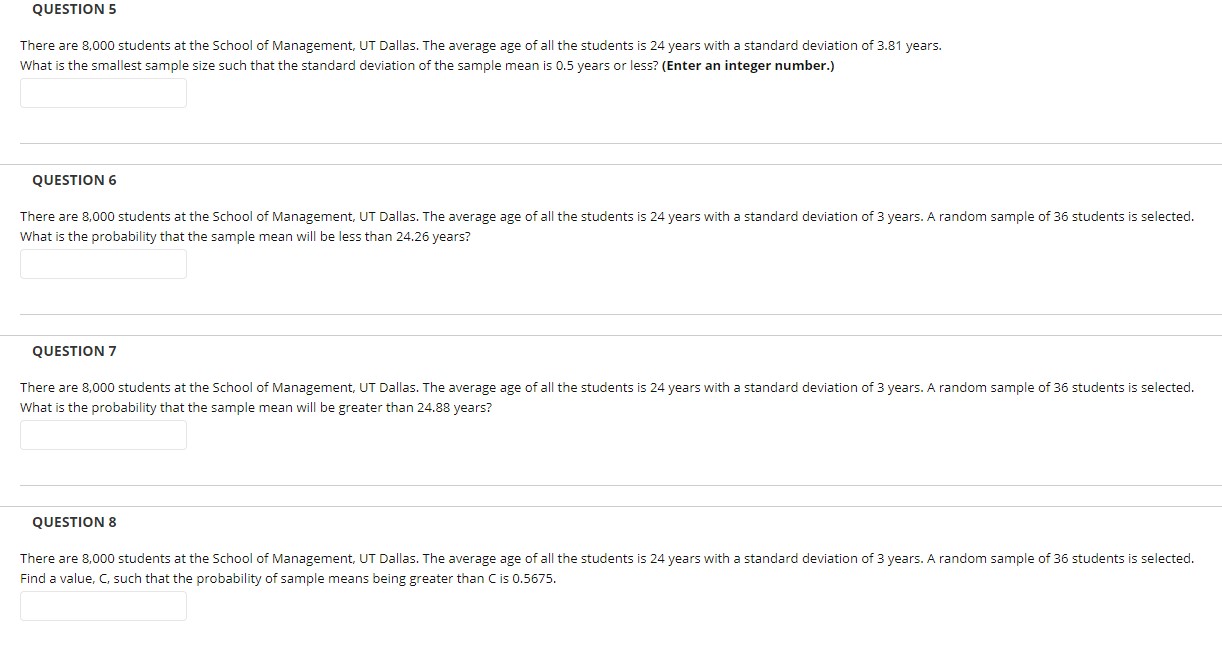
QUESTION 1 A simple random sample of 5 employees of a corporation provided the following information. Employee 1 2 3 4 5 Age 24 28 35 28 27 Gender MMF FM Compute the point estimate for the average age of all employees. QUESTION 2 A simple random sample of 5 employees of a corporation provided the following information. Employee 1 2 3 4 5 Age 26 24 35 28 27 Gender MMF FM Compute the point estimate for the standard deviation of the age of all employees. QUESTION 3 There are 8,000 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 5.1 years. A random sample of 36 students is selected. Compute the expected value of the sample mean. QUESTION 4 There are 2,593 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 3 years. A random sample of 40 students is selected. Compute the standard deviation of the sample mean.QUESTION 5 There are 8,000 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 3.81 years. What is the smallest sample size such that the standard deviation of the sample mean is 0.5 years or less? (Enter an integer number.) QUESTION 6 There are 8,000 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 3 years. A random sample of 36 students is selected. What is the probability that the sample mean will be less than 24.26 years? QUESTION 7 There are 8,000 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 3 years. A random sample of 36 students is selected. What is the probability that the sample mean will be greater than 24.88 years? QUESTION 8 There are 8,000 students at the School of Management, UT Dallas. The average age of all the students is 24 years with a standard deviation of 3 years. A random sample of 36 students is selected. Find a value, C, such that the probability of sample means being greater than C is 0.5675