please show the excel reference
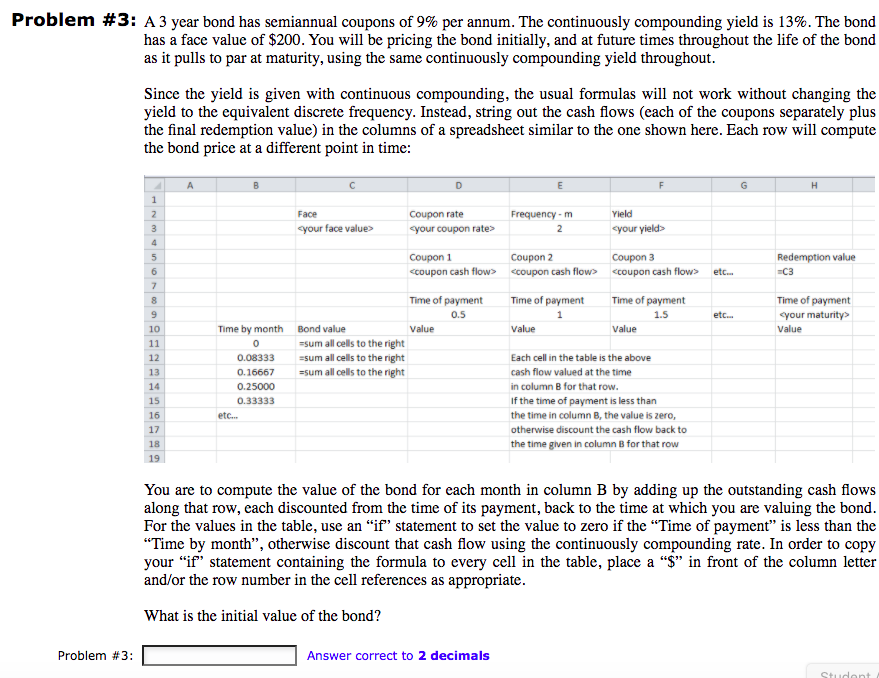
Problem #3: A 3 year bond has semiannual coupons of 9% per annum. The continuously compounding yield is 13%. The bond has a face value of $200. You will be pricing the bond initially, and at future times throughout the life of the bond as it pulls to par at maturity, using the same continuously compounding yield throughout. Since the yield is given with continuous compounding, the usual formulas will not work without changing the yield to the equivalent discrete frequency. Instead, string out the cash flows (each of the coupons separately plus the final redemption value) in the columns of a spreadsheet similar to the one shown here. Each row will compute the bond price at a different point in time: B E 1 2 3 4 Face your face value> Coupon rate your coupon rate> Frequency - m 2 Yield your yield> 5 Coupon 1 Coupon 2
Coupon 3 Redemption value -C3 etc... Time of payment 1 Value Time of payment 1.5 Value etc... Time of payment your maturity Value 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Time by month 0 0.08333 0.16667 0.25000 0.33333 etc... Time of payment 0.5 Bond value Value =sum all cells to the right =sum all cells to the right =sum all cells to the right Each cell in the table is the above cash flow valued at the time in column B for that row. if the time of payment is less than the time in column B, the value is zero, otherwise discount the cash flow back to the time given in column B for that row You are to compute the value of the bond for each month in column B by adding up the outstanding cash flows along that row, each discounted from the time of its payment, back to the time at which you are valuing the bond. For the values in the table, use an "if" statement to set the value to zero if the "Time of payment" is less than the "Time by month, otherwise discount that cash flow using the continuously compounding rate. In order to copy your ift statement containing the formula to every cell in the table, place a f in front of the column letter and/or the row number in the cell references as appropriate. What is the initial value of the bond? Problem #3: Answer correct to 2 decimals Student Problem #3: A 3 year bond has semiannual coupons of 9% per annum. The continuously compounding yield is 13%. The bond has a face value of $200. You will be pricing the bond initially, and at future times throughout the life of the bond as it pulls to par at maturity, using the same continuously compounding yield throughout. Since the yield is given with continuous compounding, the usual formulas will not work without changing the yield to the equivalent discrete frequency. Instead, string out the cash flows (each of the coupons separately plus the final redemption value) in the columns of a spreadsheet similar to the one shown here. Each row will compute the bond price at a different point in time: B E 1 2 3 4 Face your face value> Coupon rate your coupon rate> Frequency - m 2 Yield your yield> 5 Coupon 1 Coupon 2 Coupon 3 Redemption value -C3 etc... Time of payment 1 Value Time of payment 1.5 Value etc... Time of payment your maturity Value 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Time by month 0 0.08333 0.16667 0.25000 0.33333 etc... Time of payment 0.5 Bond value Value =sum all cells to the right =sum all cells to the right =sum all cells to the right Each cell in the table is the above cash flow valued at the time in column B for that row. if the time of payment is less than the time in column B, the value is zero, otherwise discount the cash flow back to the time given in column B for that row You are to compute the value of the bond for each month in column B by adding up the outstanding cash flows along that row, each discounted from the time of its payment, back to the time at which you are valuing the bond. For the values in the table, use an "if" statement to set the value to zero if the "Time of payment" is less than the "Time by month, otherwise discount that cash flow using the continuously compounding rate. In order to copy your ift statement containing the formula to every cell in the table, place a f in front of the column letter and/or the row number in the cell references as appropriate. What is the initial value of the bond? Problem #3: Answer correct to 2 decimals Student







