Please solve all parts as best as you can.

For A), I typed this out which might make more sense (inform me if it does not):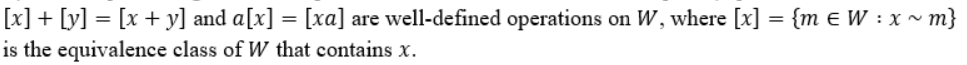

For the "W" mentioned above, that is:

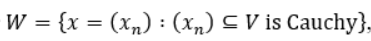
***Note: This "W" is a vector space under component-wise operations (I couldn't edit the question earlier to include it. Let me know if anything else is missed!)

Let V be a normed vector space (NVS). For the following questions, let the instance of represent an existing Banach space which contains V. o) Prove that ||[x] [y] || == lim || xn yn || is a norm on b) Let a : V where a(x) = (x,x,x...). Prove that a(V) = c) Prove that is complete when equipped with the above norm, hence we call the completion of v [x] + [y] = [x + y) and a[x] = [xa] are well-defined operations on W, where [x] = {m e W: x~m} is the equivalence class of W that contains x. W = {x = (xn) : (xn) V is Cauchy}, Let V be a normed vector space (NVS). For the following questions, let the instance of represent an existing Banach space which contains V. o) Prove that ||[x] [y] || == lim || xn yn || is a norm on b) Let a : V where a(x) = (x,x,x...). Prove that a(V) = c) Prove that is complete when equipped with the above norm, hence we call the completion of v [x] + [y] = [x + y) and a[x] = [xa] are well-defined operations on W, where [x] = {m e W: x~m} is the equivalence class of W that contains x. W = {x = (xn) : (xn) V is Cauchy}