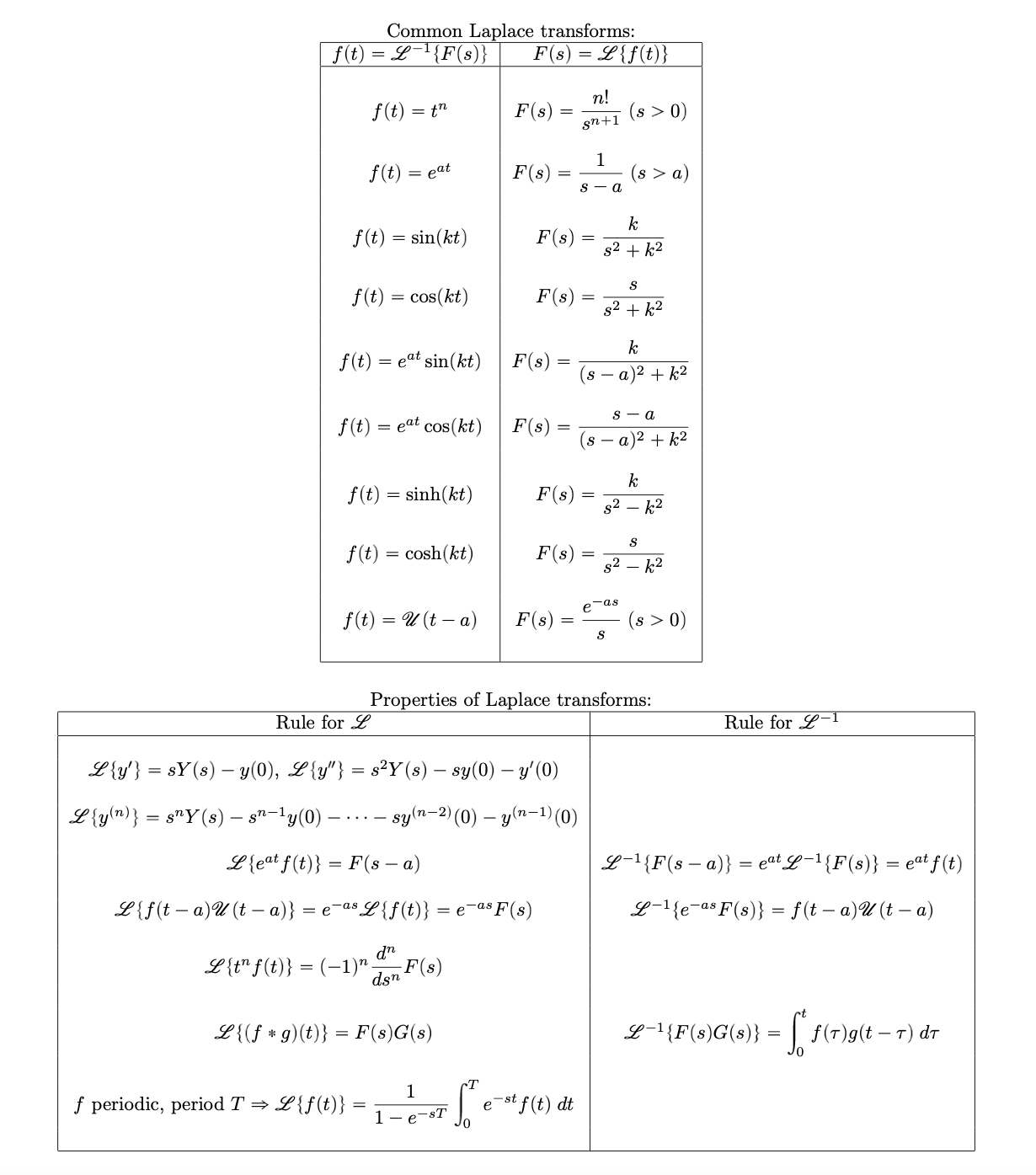
Question
Please solve below by following these steps: In summary, here are the steps for solving an initial value problem with the Laplace transform. The Laplace
Please solve below by following these steps:
In summary, here are the steps for solving an initial value problem with the Laplace transform. The Laplace table is given as the last page of this worksheet.
1. Take the Laplace transform of both sides of the equation.
2. Plug in the initial conditions and solve the new equation for Y psq ? L typtqu.
3. Take the inverse Laplace transform of both sides. You may need to use partial fraction decomposition before you can take the inverse transform.
4. This function y(t) is the solution to the original IVP.
Make sure you take the inverse Laplace transform please
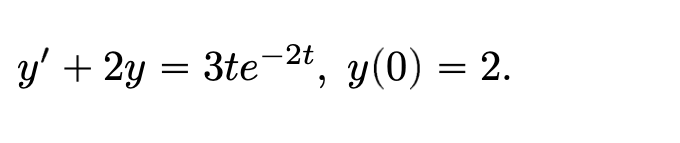
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


