Please solve these questions, there is an image below with the questions. Thanks
Explanation: The following is an application of Revenue and Cost problem in Business and Economics. You are required to apply your knowledge of the following: Construct models (find the best fit trend lines). Analyze models. . Make business decisions. Use Excel. Problem. The data in the table give sales revenues and costs and expenses for Company A for various years. Use this table to answer the following questions. Year 2003 2004 2005 2006 Sales Revenue (millions $) Cost and Expenses (millions $) 2.0523 2.3985 2.3250 2.6570 2.9578 3.8023 3.9826 4.5635 4.6687 5.2012 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 6.8524 a) Using the data set in the table, model Sales Revenues, R(x), as a quadratic function of year, with x=0 representing 2000. That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint: replace 2003 with x=3, 2004 with x=4, and so forth before plotting the graph and finding the best fit curve. Review "Module 1-Excel Applications" notes.) b) Use the function R(x) you found in part a to determine the year (round to the nearest. integer when necessary) in which the maximum revenue occurs, and then compare this value with the real data (maximum revenue in the table). 1 of 2 Assignment 1 4.9850 5.1256 2.5986 2.9102 4.7563 4.4987 4.3250 4.2052 3.9875 3.5230 3.8753 4.0453 4.8658 4.9223 4.6754 5.4012 5.7253 6.6571 6.7523 c) Write a sentence to describe how well the function fits the data. d) Using the data set in the table, model Cost and Expenses, C(x), as a quadratic function of year, with x=0 representing 2000. That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint: replace 2003 with x=3, 2004 with x=4, and so on, before plotting the graph and finding the best fit curve.) Continued on the next page... e) Using the data set in the table, model Profit function, P(x), as a quadratic. Would a quadratic model be a good fit? Why? (Use Excel) f) According to the profit function's "graph" you found in part e, in which year maximum profit occurs, and what is the maxim profit? g) Through the decade from 2008 to 2017, does the function P(x) project increasing or decreasing profits? Do the real data support this trend? Why? h) How might management respond to this kind of projection? Be specific while you explain your suggestions: use terms like "minimizing cost", "increasing revenue", "maximizing profit", "in the short/long term", etc., in your sentences.
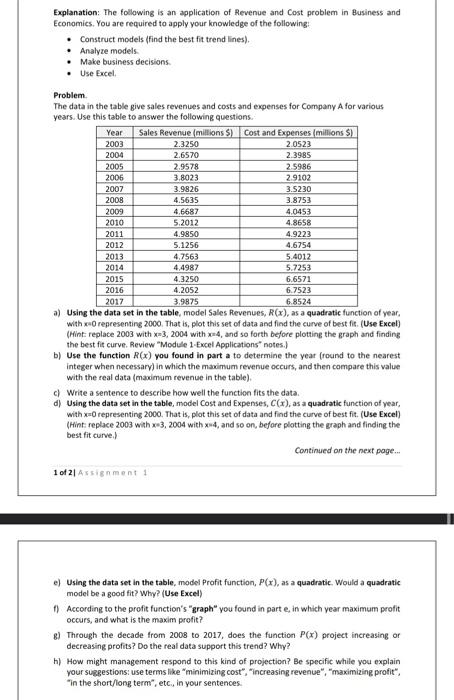
Begin from question a, desgin the revenue function using the given data and go from there to solve the other questions.
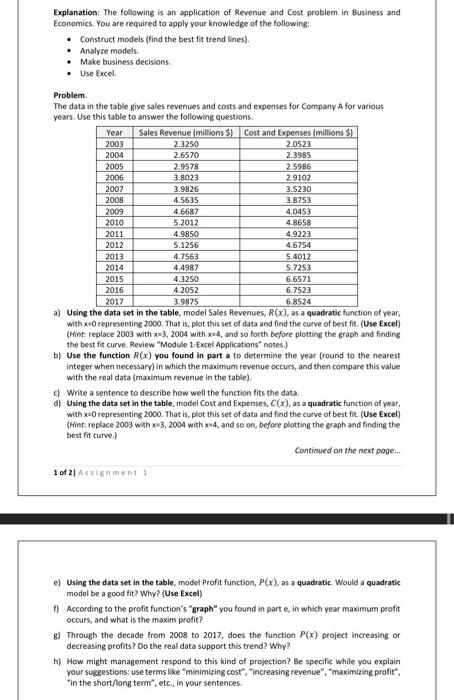
Explanation: The following is an application of Revenue and Cost problem in Business and Economics. You are required to apply your knowledge of the following: - Construct models (find the best fit trend lines). - Analyze models. - Make business decisions. - Use Eacel. Problem. The data in the table give sales revenues and costs and expenses for Company A for various years. Use this table to answer the following questions. a) Using the data set in the table, model Sales Fevenues, R(x), as a quadratic function of year, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fis. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so forth bejore plotting the graph and finding the best fit curve. Review "Module 1-Excel Applications" notes.) b) Use the function R(x) you found in part a to determine the year (round to the nearest integer when necessary) in which the maximum revenue occurs, and then compare this value with the real data (maximum revenue in the table). c) Write a sentence to describe how well the function fits the data. d) Using the data set in the table, model Cost and Expenses, C(x), as a quadratic function of vear, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint replace 2003 with x=3,2004 with x=4, and so on, before plotting the graph and finding the best fit curve, Continued on the next page... 1 of 2 is sigin min en i 1 e) Using the data set in the table, model Profit function, P(x), as a quadratic. Would a quadratic model be a good fit? Why? (Use Excel) f) According to the profit function's "graph" you found in part e, in which year maximum profit occurs, and what is the maxim profit? g) Through the decade from 2008 to 2017 , does the function P(r) project increasing or decreasing profits? Do the real data support this trend? Why? h) How might management respond to this kind of projection? Be specific while you explain vour suggestions: use terms like "minimizing cost", "increasing revenue", "maximizing protit", "in the short/iong term", etc. in your sentences. Explanation: The following is an application of Revenue and Cost problem in Business and Economics. You are required to apply your knowledge of the following: - Construct models (find the best fit trend lines). - Analyze models. - Make business decisions. - Use Excel. Problem. The data in the table give sales revenues and costs and expenses for Company A for various years. Use this table to answer the following questions. a) Using the data set in the table, model Sales Hevenues, K(x), as a quadratic function of year, with xo0 representing 2000 . That is, plot this set of data and find the curve of best fis. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so forth bejore plotting the graph and finding the best fis curve. Review "Module 1-Excel Applications" notes.) b) Use the function R(x) you found in part a to determine the year fround to the nearest integer when necessary) in which the maximum revenue occurs, and then compare this value with the real data (maximum revenue in the table). c) Write a sentence to describe how well the function fits the data. d) Using the data set in the table, model Cost and Expenses, C(x), as a quadratic functioe of year, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so on, before plotting the graph and finding the best fit curve. Continued on the next page... 1 of 21 As signnent 1 e) Using the data set in the table, model Profit function, P(x), as a quadratic. Would a quadratic model be a good fit? Why? (Use Excel) f) According to the profit function's "graph" you found in part e, in which year maximum profit occurs, and what is the maxim profit? g) Through the decade from 2008 to 2017 , does the function P(x) project increasing or decreasing profits? Do the real data support this trend? Why? h) How might management respond to this kind of projection? Be specific while you explain your suzgestions: use terms like "minimizing cost", "increasing revenue", "maximizing protit", "in the short/iong term", etc., in your sentences. Explanation: The following is an application of Revenue and Cost problem in Business and Economics. You are required to apply your knowledge of the following: - Construct models (find the best fit trend lines). - Analyze models. - Make business decisions. - Use Eacel. Problem. The data in the table give sales revenues and costs and expenses for Company A for various years. Use this table to answer the following questions. a) Using the data set in the table, model Sales Fevenues, R(x), as a quadratic function of year, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fis. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so forth bejore plotting the graph and finding the best fit curve. Review "Module 1-Excel Applications" notes.) b) Use the function R(x) you found in part a to determine the year (round to the nearest integer when necessary) in which the maximum revenue occurs, and then compare this value with the real data (maximum revenue in the table). c) Write a sentence to describe how well the function fits the data. d) Using the data set in the table, model Cost and Expenses, C(x), as a quadratic function of vear, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint replace 2003 with x=3,2004 with x=4, and so on, before plotting the graph and finding the best fit curve, Continued on the next page... 1 of 2 is sigin min en i 1 e) Using the data set in the table, model Profit function, P(x), as a quadratic. Would a quadratic model be a good fit? Why? (Use Excel) f) According to the profit function's "graph" you found in part e, in which year maximum profit occurs, and what is the maxim profit? g) Through the decade from 2008 to 2017 , does the function P(r) project increasing or decreasing profits? Do the real data support this trend? Why? h) How might management respond to this kind of projection? Be specific while you explain vour suggestions: use terms like "minimizing cost", "increasing revenue", "maximizing protit", "in the short/iong term", etc. in your sentences. Explanation: The following is an application of Revenue and Cost problem in Business and Economics. You are required to apply your knowledge of the following: - Construct models (find the best fit trend lines). - Analyze models. - Make business decisions. - Use Excel. Problem. The data in the table give sales revenues and costs and expenses for Company A for various years. Use this table to answer the following questions. a) Using the data set in the table, model Sales Hevenues, K(x), as a quadratic function of year, with xo0 representing 2000 . That is, plot this set of data and find the curve of best fis. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so forth bejore plotting the graph and finding the best fis curve. Review "Module 1-Excel Applications" notes.) b) Use the function R(x) you found in part a to determine the year fround to the nearest integer when necessary) in which the maximum revenue occurs, and then compare this value with the real data (maximum revenue in the table). c) Write a sentence to describe how well the function fits the data. d) Using the data set in the table, model Cost and Expenses, C(x), as a quadratic functioe of year, with x=0 representing 2000 . That is, plot this set of data and find the curve of best fit. (Use Excel) (Hint: replace 2003 with x=3,2004 with x=4, and so on, before plotting the graph and finding the best fit curve. Continued on the next page... 1 of 21 As signnent 1 e) Using the data set in the table, model Profit function, P(x), as a quadratic. Would a quadratic model be a good fit? Why? (Use Excel) f) According to the profit function's "graph" you found in part e, in which year maximum profit occurs, and what is the maxim profit? g) Through the decade from 2008 to 2017 , does the function P(x) project increasing or decreasing profits? Do the real data support this trend? Why? h) How might management respond to this kind of projection? Be specific while you explain your suzgestions: use terms like "minimizing cost", "increasing revenue", "maximizing protit", "in the short/iong term", etc., in your sentences









