please solve this question :

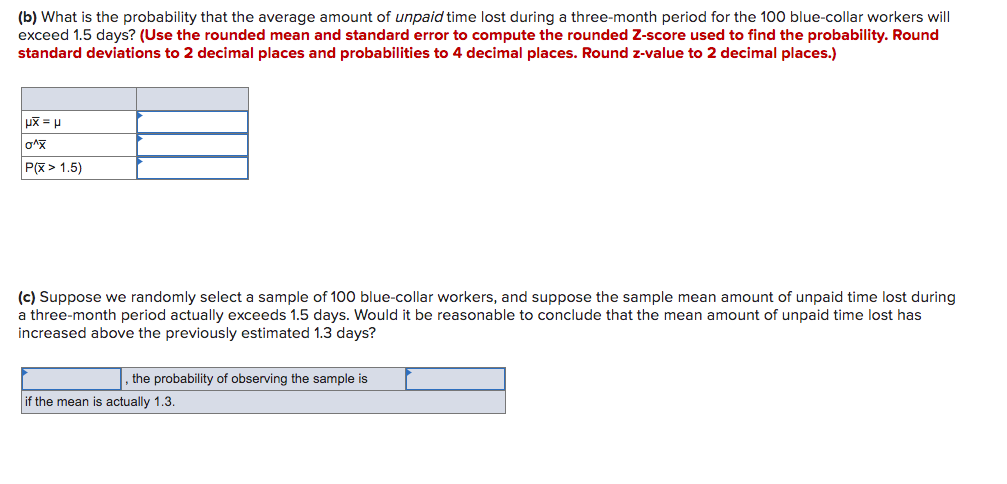
In an article in the Journal of Management, Joseph Martocchio studied and estimated the costs of employee absences. Based on a sample of 176 blue-collar workers, Martocchio estimated that the mean amount of paid time lost during a three-month period was 1.0 days per employee with a standard deviation of 1.2 days. Martocchio also estimated that the mean amount of unpaid time lost during a three-month period was 1.3 day per employee with a standard deviation of 1.5 days. Suppose we randomly select a sample of 100 blue-collar workers. Based on Martocchio's estimates: (a) What is the probability that the average amount of paid time lost during a three-month period for the 100 blue-collar workers will exceed 1.5 days? (Use the rounded mean and standard error to compute the rounded Z-score used to find the probability. Round means to 1 decimal place, standard deviations to 2 decimal places, and probabilities to 4 decimal places. Round z-value to 2 decimal places.) UX = H P(x > 1.5) (b) What is the probability that the average amount of unpaid time lost during a three-month period for the 100 blue-collar workers will exceed 1.5 days? (Use the rounded mean and standard error to compute the rounded Z-score used to find the probability. Round standard deviations to 2 decimal places and probabilities to 4 decimal places. Round z-value to 2 decimal places.) HX = Hlb} What is the probability that the average amount of unpaid time lost during a three-month period for the 100 blue-collar workers will exceed 1.5 days? (Use the rounded mean and standard error to compute the rounded Z-score used to find the probability. Round standard deviations to 2 decimal places and probabilities to 4 decimal places. Round z-value to 2 decimal places] Hi: 11 0R P07: 1.5} [1:] Suppose we randomly select a sample of100 blue-collar workers, and suppose the sample mean amount of unpaid time lost during a three-month period actually exceeds 1.5 days. Would it be reasonable to conclude that the mean amount of unpaid time lost has increased above the previously estimated 1.3 days? . the probability of observing the sample is if the mean is aohjally 1.3