please solve using excel solver
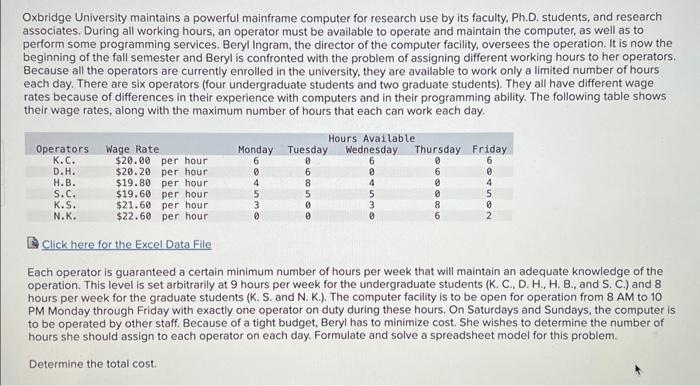
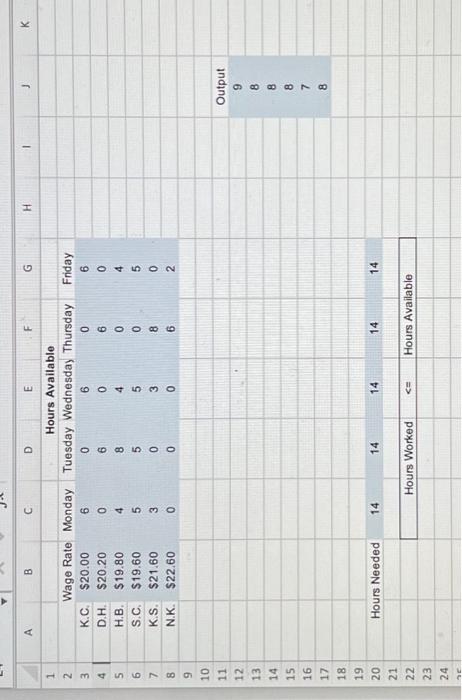
Oxbridge University maintains a powerful mainframe computer for research use by its faculty, Ph.D. students, and research associates. During all working hours, an operator must be available to operate and maintain the computer, as well as to perform some programming services. Beryl Ingram, the director of the computer facility, oversees the operation. It is now the beginning of the fall semester and Beryl is confronted with the problem of assigning different working hours to her operators. Because all the operators are currently enrolled in the university, they are available to work only a limited number of hours each day. There are six operators (four undergraduate students and two graduate students). They all have different wage rates because of differences in their experience with computers and in their programming ability. The following table shows their wage rates, along with the maximum number of hours that each can work each day. Click here for the Excel Data File Each operator is guaranteed a certain minimum number of hours per week that will maintain an adequate knowledge of the operation. This level is set arbitrarily at 9 hours per week for the undergraduate students (K. C., D. H., H. B., and S. C.) and 8 hours per week for the graduate students (K.S. and N. K.). The computer facility is to be open for operation from 8AM to 10 PM Monday through Friday with exactly one operator on duty during these hours. On Saturdays and Sundays, the computer is to be operated by other staff. Because of a tight budget, Beryl has to minimize cost. She wishes to determine the number of hours she should assign to each operator on each day. Formulate and solve a spreadsheet model for this problem. Determine the total cost. \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline & A & B & C & D & E & F & G & H & 1 & J & K \\ \hline 1 & E & & & \multicolumn{3}{|c|}{ Hours Available } & & & & & \\ \hline 2 & \multicolumn{2}{|r|}{ Wage Rate } & Monday & Tuesday & Wednesday & Thursday & Friday & & & & \\ \hline 3 & K.C. & $20.00 & 6 & 0 & 6 & 0 & 6 & & & & \\ \hline 4 & D.H. & $20.20 & 0 & 6 & 0 & 6 & 0 & & & & \\ \hline 5 & H.B. & $19.80 & 4 & 8 & 4 & 0 & 4 & & & & \\ \hline 6 & S.C. & $19.60 & 5 & 5 & 5 & 0 & 5 & & & & \\ \hline 7 & K.S. & $21.60 & 3 & 0 & 3 & 8 & 0 & & & & \\ \hline 8 & N.K. & $22.60 & 0 & 0 & 0 & 6 & 2 & & & & \\ \hline 9 & & a & & & & & & & & & \\ \hline \multicolumn{12}{|l|}{10} \\ \hline 11 & & & & & & & i. & & & Output & \\ \hline 12 & & & & & (1.. & & & & & 9 & \\ \hline \multicolumn{12}{|l|}{13} \\ \hline 14 & & & & & & & & & & 8 & \\ \hline \multicolumn{12}{|l|}{15} \\ \hline \multicolumn{12}{|l|}{16} \\ \hline 17 & & & & & & 10 & 4 & & & 8 & \\ \hline \multicolumn{12}{|l|}{18} \\ \hline \multicolumn{12}{|l|}{19} \\ \hline 20 & \multicolumn{2}{|c|}{ Hours Needed } & 14 & 14 & 14 & 14 & 14 & & & & \\ \hline \multicolumn{12}{|l|}{21} \\ \hline 22 & & & \multicolumn{2}{|c|}{ Hours Worked } &