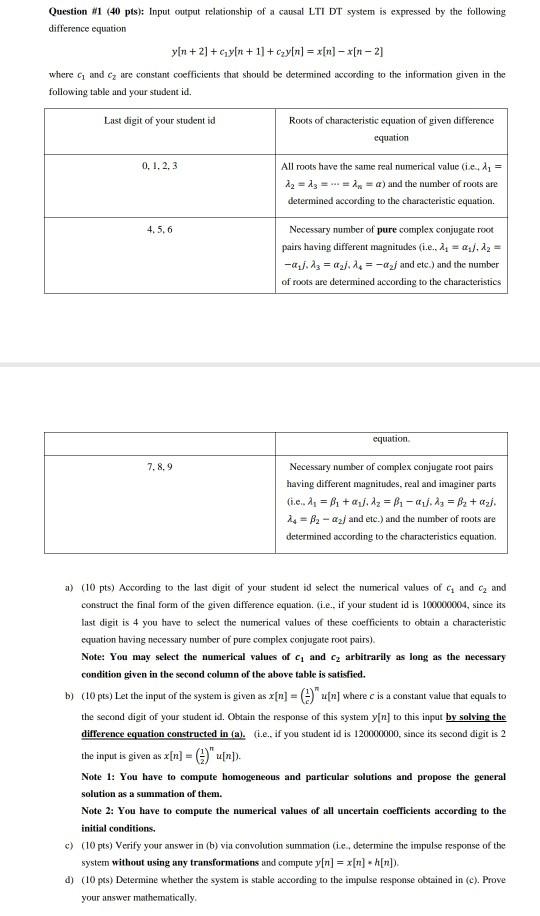
Please take last digit=4 Second digit=6

Question #1 (40 pts): Input output relationship of a causal LTI DT system is expressed by the following difference equation yin +2] + cyfn + 1] + czy[n] = *[n] x[n- 2] where G and ca are constant coefficients that should be determined according to the information given in the following table and your student id. Lust digit of your student id Roots of characteristic equation of given difference equation 0.1.2.3 All roots have the same real numerical value (ie, dy = 12 = 13 = ... = n = a) and the number of roots are determined according to the characteristic equation. 4,5,6 Necessary number of pure complex conjugate root pairs having different magnitudes (i... 12 = , 12 = -aj. 13 = a ), 19 = -anj and etc.) and the number of roots are determined according to the characteristics equution 7.8.9 Necessary number of complex conjugate root pairs having different magnitudes, real and imaginer parts (... A, = B1 + a), 12 = B1 - 1). Az = B2 + az/ is = B2 - az and etc.) and the number of roots are determined according to the characteristics equation. a) (10 pts) According to the last digit of your student id select the numerical values of G and C and construct the final form of the given difference equation. (i.e., if your student id is 100000004, since its last digit is 4 you have to select the numerical values of these coefficients to obtain a characteristic equation having necessary number of pure complex conjugate root pairs). Note: You may select the numerical values of c, and cz arbitrarily as long as the necessary condition given in the second column of the above table is satisfied. b) (10 pts) Let the input of the system is given as x[n] = ?) u[n] where c is a constant value that equals to the second digit of your student id. Obtain the response of this system y[n] to this input by solving the difference equation constructed in (a). (i.e., if you student id is 120000000, since its second digit is 2 the input is given as x[n] = {"u[n). Note 1: You have to compute homogeneous and particular solutions and propose the general solution as a summation of them. Note 2: You have to compute the numerical values of all uncertain coefficients according to the initial conditions. c) (10 pts) Verify your answer in (b) via convolution summation (ie, determine the impulse response of the system without using any transformations and compute y[n] = x[n] -h[n]). d) (10 pts) Determine whether the system is stable according to the impulse response obtained in (c). Prove your answer mathematically Question #1 (40 pts): Input output relationship of a causal LTI DT system is expressed by the following difference equation yin +2] + cyfn + 1] + czy[n] = *[n] x[n- 2] where G and ca are constant coefficients that should be determined according to the information given in the following table and your student id. Lust digit of your student id Roots of characteristic equation of given difference equation 0.1.2.3 All roots have the same real numerical value (ie, dy = 12 = 13 = ... = n = a) and the number of roots are determined according to the characteristic equation. 4,5,6 Necessary number of pure complex conjugate root pairs having different magnitudes (i... 12 = , 12 = -aj. 13 = a ), 19 = -anj and etc.) and the number of roots are determined according to the characteristics equution 7.8.9 Necessary number of complex conjugate root pairs having different magnitudes, real and imaginer parts (... A, = B1 + a), 12 = B1 - 1). Az = B2 + az/ is = B2 - az and etc.) and the number of roots are determined according to the characteristics equation. a) (10 pts) According to the last digit of your student id select the numerical values of G and C and construct the final form of the given difference equation. (i.e., if your student id is 100000004, since its last digit is 4 you have to select the numerical values of these coefficients to obtain a characteristic equation having necessary number of pure complex conjugate root pairs). Note: You may select the numerical values of c, and cz arbitrarily as long as the necessary condition given in the second column of the above table is satisfied. b) (10 pts) Let the input of the system is given as x[n] = ?) u[n] where c is a constant value that equals to the second digit of your student id. Obtain the response of this system y[n] to this input by solving the difference equation constructed in (a). (i.e., if you student id is 120000000, since its second digit is 2 the input is given as x[n] = {"u[n). Note 1: You have to compute homogeneous and particular solutions and propose the general solution as a summation of them. Note 2: You have to compute the numerical values of all uncertain coefficients according to the initial conditions. c) (10 pts) Verify your answer in (b) via convolution summation (ie, determine the impulse response of the system without using any transformations and compute y[n] = x[n] -h[n]). d) (10 pts) Determine whether the system is stable according to the impulse response obtained in (c). Prove your answer mathematically