Please take note that we are not supposed to use loops in the implementation of recursion methods. Also in the sample output, the "Sum up to fibonacci(30) is NOT 24961200 but rather 2178308. Other than that everything is as described on the pages. Thank you in advance.
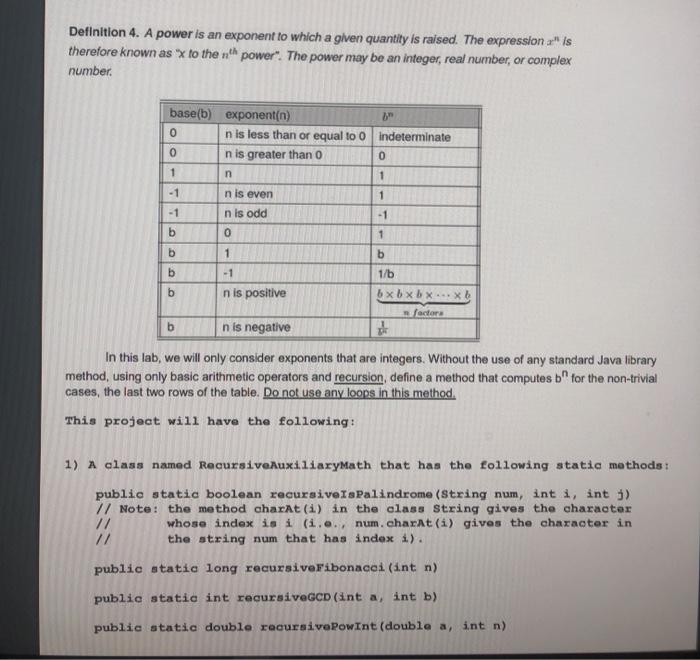
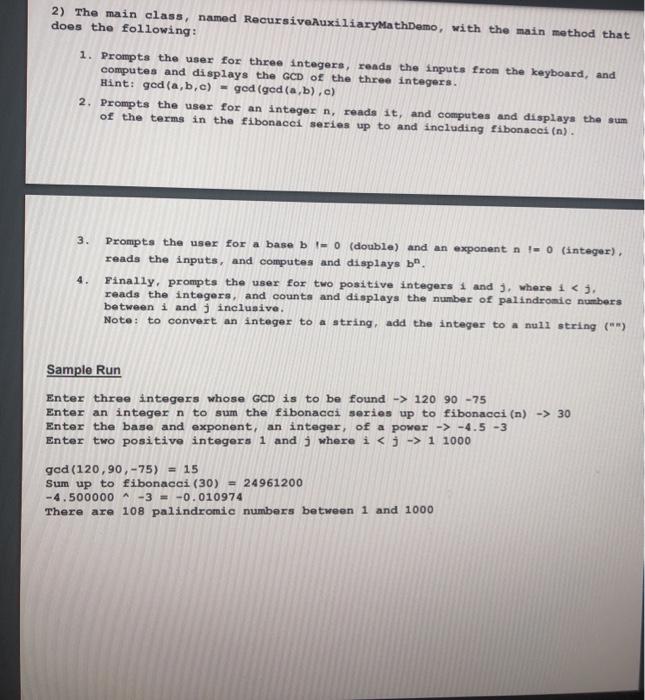
CSC 1351-2. Spring 2021. Lab 4 Name this project Recursive Auxiliary Math NOTE: Implement the following 4 methods using recursion. Do not use any loops in the implementation of these 4 methods. Definition 1. A palindromic number is a non-negative integer which stays the same when its digits are reversed. Both 159951 and 4782874 are palindromic numbers but 12345321 is not. Definition 2. The Fibonacci numbers are the numbers in the following integer sequence: 0,1,1,2,3,5,8,13,21,34,55,.... By definition, fibonacci(0) = 0, fibonacci(1) = 1, and each subsequent number is the sum of the previous two Definition 3. The greatest common denominator, denoted GCD. of two or more integers is the largest positive Integer that can evenly divide the numbers. For example, the GCD of 12, 15 and 30 is 3. When computing the GCD of two integers, If exactly one of the number is 0, their GCD is the non-zero number. When computing the GCD of two numbers, if both numbers are o, their GCD is indeterminate. GCD Algorithm Input : a, b: Integer output: ged(a,b) intialization: If a 0 AND b =0 then god -- NaN; else if a = 0 OR b 0 then god - la +41 else alol: 16: while bo do rt-remainder(a,b); ab: b end woda end Definition 4. A power is an exponent to which a given quantity is raised. The expression x" is therefore known as "x to the power". The power may be an integer, real number, or complex number base(b) exponent(n) 0 n is less than or equal to 0 indeterminate 0 n is greater than 0 0 1 n 1 -1 n is even 1 -1 n is odd - 1 b 0 1 1 b OOO - 1 n is positive 1/b bxbxbx... x factors b n is negative In this lab, we will only consider exponents that are integers. Without the use of any standard Java library method, using only basic arithmetic operators and recursion, define a method that computes b" for the non-trivial cases, the last two rows of the table. Do not use any loops in this method. This project will have the following: 1) A class named RecursiveAuxiliarymath that has the following static methods: public static boolean recursiveIsPalindrome (String num, int i, int i) 7/ Note: the method charAt(i) in the class String gives the character whose index is i (i..., num.charAt(1) gives the character in the string num that has index 1). public static long recursiveFibonacci (int n) public static int recursiveGCD (int a, int b) public static double recursivoPowInt (double a, int n) 2) The main class, named RecursiveAuxiliaryMathDemo, with the main method that does the following: 1. Prompts the user for three integers, reads the inputs from the keyboard, and computes and displays the GCD of the three integers. Hint: ged(a,b,c) = god (ged (a,b), c) 2. Prompts the user for an integer n, roads it, and computes and displays the sum of the terms in the fibonacci series up to and including fibonacci (n). 3. 4. Prompts the user for a base b0 (double) and an exponent n = 0 (integer), reads the inputs, and computes and displays b. Finally, prompts the user for two positive integers 1 and 3, where i cj. reads the integers, and counts and displays the number of palindromic numbers between i and j inclusive. Note: to convert an integer to a string, add the integer to a null string (**) Sample Run Enter three integers whose GCD is to be found -> 120 90 -75 Enter an integer n to sum the fibonacci series up to fibonacci (n) -> 30 Enter the base and exponent, an integer, of a power -> -4.5 -3 Enter two positive integers 1 and where is j -> 1 1000 god (120,90,-75) = 15 Sum up to fibonacci (30) = 24961200 -4.500000-3 = -0.010974 There are 108 palindromic numbers between 1 and 1000