Please take your time and let me know if you have any questions. Thank you so much for the help! I will upvote right away.
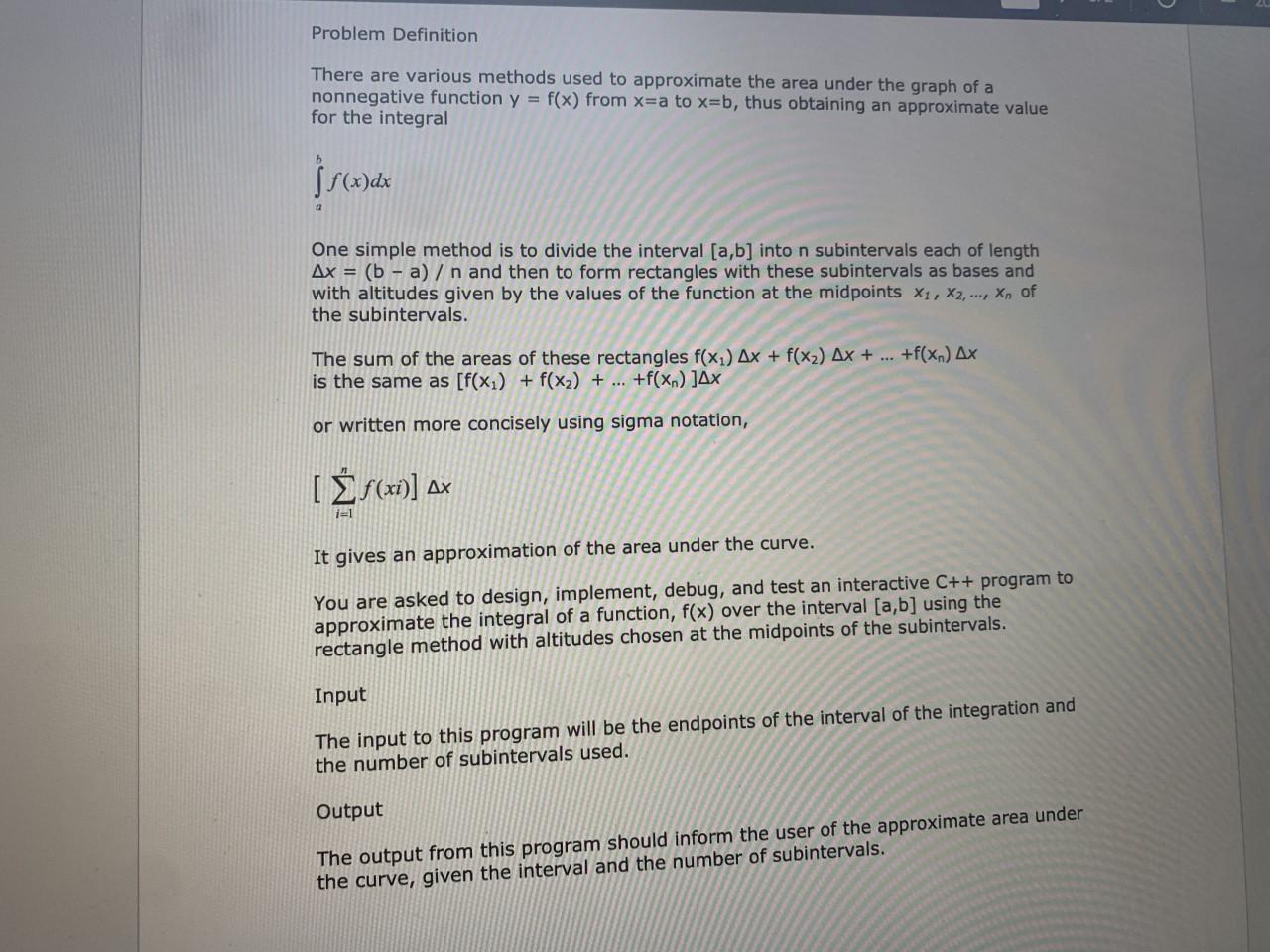

Problem Definition There are various methods used to approximate the area under the graph of a nonnegative function y = f(x) from x=a to x=b, thus obtaining an approximate value for the integral } (x) dx One simple method is to divide the interval [a,b] into n subintervals each of length Ax = (b - a) / n and then to form rectangles with these subintervals as bases and with altitudes given by the values of the function at the midpoints X1, X2, ..., Xn of the subintervals. The sum of the areas of these rectangles f(x1) Ax + f(x2) Ax + ... +f(x) Ax is the same as [f(x) + f(x) + ... +f(xn) ]AX or written more concisely using sigma notation, /(x)] 2x 11 It gives an approximation of the area under the curve. You are asked to design, implement, debug, and test an interactive C++ program to approximate the integral of a function, f(x) over the interval [a,b] using the rectangle method with altitudes chosen at the midpoints of the subintervals. Input The input to this program will be the endpoints of the interval of the integration and the number of subintervals used. Output The output from this program should inform the user of the approximate area under the curve, given the interval and the number of subintervals. Additional Notes: 1. Here is the function you are evaluating: f(x) 1 if x 1 2. The required external documentation is a problem definition and word- processed variable list and algorithm for each function. Use the external documentation template provided in Canvas. Problem Description: Main Function Variable List Main Function Algorithm Programmer-Defined Function (used only when your program contains a function other than the main function) Name: Type: Argument List: Local Variables: Pre-Condition(s): Algorithm: Problem Definition There are various methods used to approximate the area under the graph of a nonnegative function y = f(x) from x=a to x=b, thus obtaining an approximate value for the integral } (x) dx One simple method is to divide the interval [a,b] into n subintervals each of length Ax = (b - a) / n and then to form rectangles with these subintervals as bases and with altitudes given by the values of the function at the midpoints X1, X2, ..., Xn of the subintervals. The sum of the areas of these rectangles f(x1) Ax + f(x2) Ax + ... +f(x) Ax is the same as [f(x) + f(x) + ... +f(xn) ]AX or written more concisely using sigma notation, /(x)] 2x 11 It gives an approximation of the area under the curve. You are asked to design, implement, debug, and test an interactive C++ program to approximate the integral of a function, f(x) over the interval [a,b] using the rectangle method with altitudes chosen at the midpoints of the subintervals. Input The input to this program will be the endpoints of the interval of the integration and the number of subintervals used. Output The output from this program should inform the user of the approximate area under the curve, given the interval and the number of subintervals. Additional Notes: 1. Here is the function you are evaluating: f(x) 1 if x 1 2. The required external documentation is a problem definition and word- processed variable list and algorithm for each function. Use the external documentation template provided in Canvas. Problem Description: Main Function Variable List Main Function Algorithm Programmer-Defined Function (used only when your program contains a function other than the main function) Name: Type: Argument List: Local Variables: Pre-Condition(s): Algorithm









