please to write matlab code.
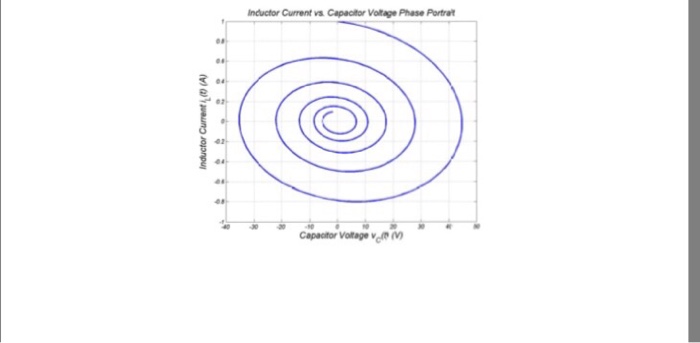
Objective: To gain experience in using MATLAB as a programming language. To use MATLAB to simulate the response of electrical circuits. Background: The behavior of the series RLC circuit introduced in MATLAB Exercise 4 can also be characterized by a pair of coupled first-order differential equations involving the capacitor voltage ve() and inductor current i (t) dive() dt di (t) e() i (0) i (A) Here we are interested in finding a solution for v (t) and i in the source-free case V. 0V) starting from specified initial conditions ve(0) v, v) and i(0) i, (A). The total energy stored in this circuit is the sum of the energy stored in the capacitor's electric field and the energy stored in the inductor's electric field, given as: (i) Engineers often use computer-aided numerical techniques to derive approximate solutions. One approach is to discretize the differential equations to yield difference equations that characterize the solutions at discrete instants in time. A straightforward way to do this is to approximate the derivatives on the left-hand sides of the differential equations by the forward differences: dve() di i (t AM) -i (t) in which Ar is the step size parameter. The smaller the step size parameter value, the better the approximation to the true derivative. Then, the so-called Euler discretization scheme is obtained by evaluating the continuous time variable t at multiples of the step size parameter, ie. kau for k 0,1,2,..., along with using the above derivative approximations. This leads to: v (k +1)A)- v (AAM) i (AA) ve(kA) At Objective: To gain experience in using MATLAB as a programming language. To use MATLAB to simulate the response of electrical circuits. Background: The behavior of the series RLC circuit introduced in MATLAB Exercise 4 can also be characterized by a pair of coupled first-order differential equations involving the capacitor voltage ve() and inductor current i (t) dive() dt di (t) e() i (0) i (A) Here we are interested in finding a solution for v (t) and i in the source-free case V. 0V) starting from specified initial conditions ve(0) v, v) and i(0) i, (A). The total energy stored in this circuit is the sum of the energy stored in the capacitor's electric field and the energy stored in the inductor's electric field, given as: (i) Engineers often use computer-aided numerical techniques to derive approximate solutions. One approach is to discretize the differential equations to yield difference equations that characterize the solutions at discrete instants in time. A straightforward way to do this is to approximate the derivatives on the left-hand sides of the differential equations by the forward differences: dve() di i (t AM) -i (t) in which Ar is the step size parameter. The smaller the step size parameter value, the better the approximation to the true derivative. Then, the so-called Euler discretization scheme is obtained by evaluating the continuous time variable t at multiples of the step size parameter, ie. kau for k 0,1,2,..., along with using the above derivative approximations. This leads to: v (k +1)A)- v (AAM) i (AA) ve(kA) At