Answered step by step
Verified Expert Solution
Question
1 Approved Answer
PLEASE USING MATLAB Consider the localization toy example discussed in lecture with three beacons with locations specified by the coordinates (x1,y1),(x2,y2),(x3,y3). Unlike the lecture example,
PLEASE USING MATLAB 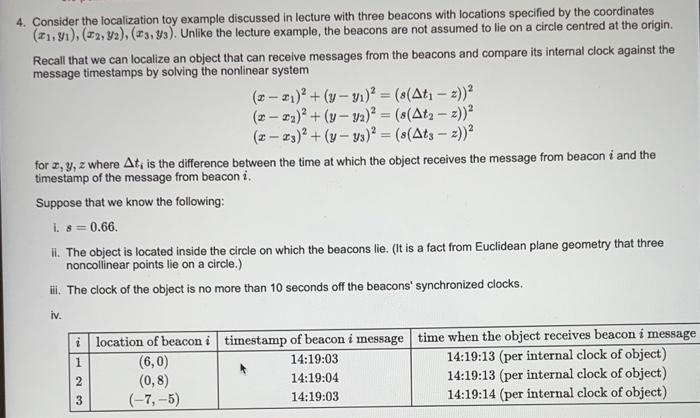


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


