Please write codes which satisfy the following conditions in Python 3.

Thank you very much for your help.

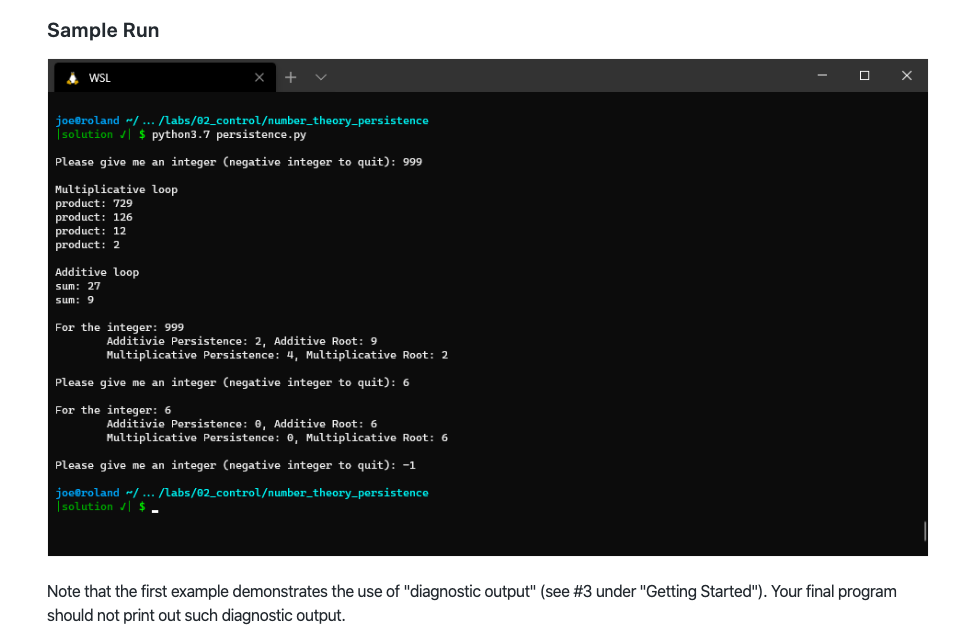
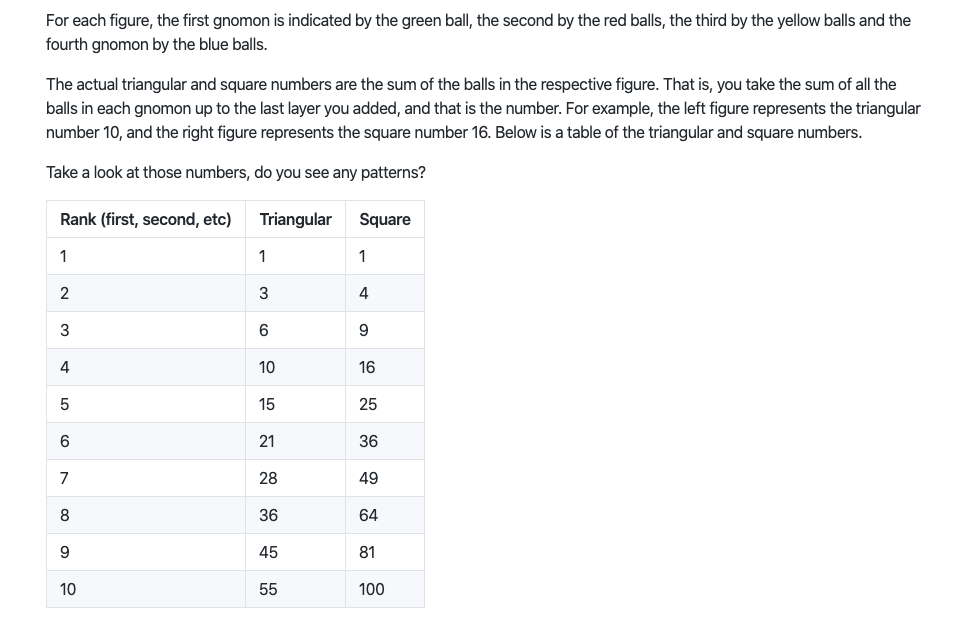
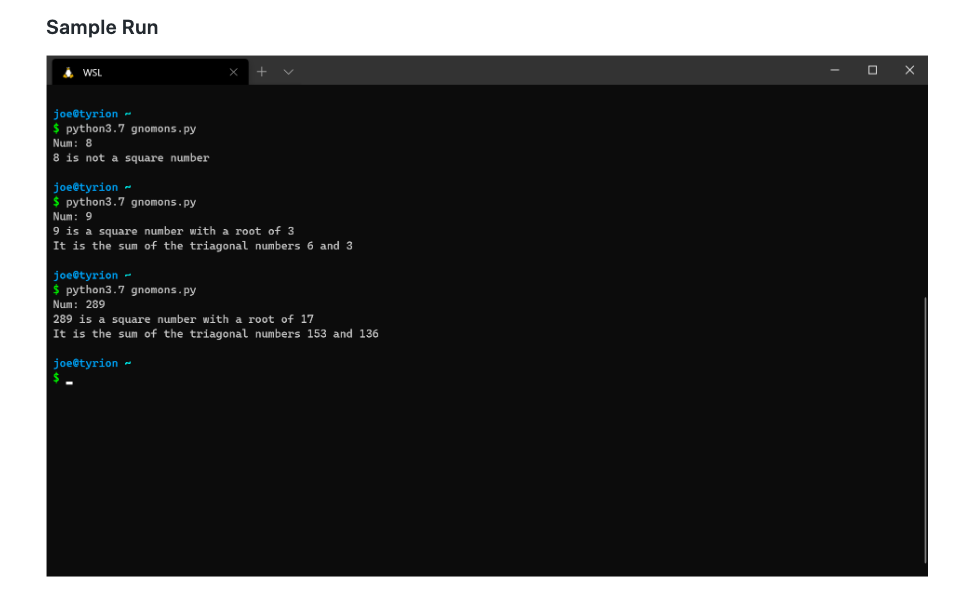
Number Theory - Additive & Multiplicative Persistence Assignment Overview The aim of this project is practice the use of while loops and conditional statements. You are going to write a program that prompts the user for an integer and then determines the additive persistence and corresponding additive root, and the multiplicative persistence, the corresponding multiplicative digital root of that integer. You will continue to do so until the user quits. Background There are many properties of numbers that one can investigate. The ancient Greeks were fascinated with the properties of integers, even ascribing them mystical properties. One such property is an integer's additive persistence and its resulting additive digital root. Additive persistence is a property of the sum of the digits of an integer. The sum of the digits is found, and then the summation of digits is performed on the sum, repeating until a single integer digit is reached. The number of such cycles is that integer's additive persistence. Consider the following example: 1. The beginning integer is 1234 2. Sum its digits is 1+2+3+4 = 10 3. The integer is now 10 4. The sum of its digits is 1 + 0 = 1 5. The integer is 1. When the value reaches a single digit, we are finished. This final integer is the additive root The number of cycles is the additive persistence. The integer 1234 has an additive persistence of 2 (first sum was 10, then the second sum was 1). The final digit reached is called the integer's additive digital root. The digital root of 1234 is 1. The multiplicative persistenceand resulting multiplicative digital root are determined the same way, only multiplying the digits of an integer instead of adding. For example: 1. The beginning integer is 1234 2. The product of 123*4 = 24 3. The integer is now 24 4. The product of 2*4 = 8 5. The integer is now 8. When the value reaches a single digit, we are finished. This final integer is the multiplicative root. As before, the number of cycles is the multiplicative persistence. For 1234, the multiplicative persistence is 2, and its multiplicative root is 8. Problem Statement The program should run as follows: 1. Ask the user for an integer. 2. If the given integer is a single digit, report it's additive persistence and multiplicative persistence as 0 and both its additive and multiplicative root as itself. 3. If the integer is less than 0, that is a signal to quit the program. 4. Otherwise, find the additive/multiplicative persistence and additive/multiplicative root of the given integer and report the results to the user 5. Continue by prompting the user until they quit. Deliverables The deliverable for this assignment is the following file: persistence.py -- your solution source code Be sure to use the specified file name. Getting Started 1. Break the problem down into parts. Some obvious parts: i. Gather input from the user, and check for negative numbers (the quit condition) ii. Write a loop around the queries that can do the queries until the stop condition is reached iii. Write a loop that can sum the digits of an integer until it reaches a single digit. iv. Write a loop that can take the produce of the digits of an integer until it reaches a single digit, using the above approach v. Get the whole thing to work with one or the other (additive, multiplicative) before you address the other 2. How do you get the digits of an integer? Look at a combination of division (/) and remainder(%) operators on integers. 3. I would add some "diagnostic output" so you can be sure things are working as they should. For each pass through the loop of the additive (or multiplicative) persistence, print each new integer created Sample Run WSL x + V - O X joe@roland solution / ... /labs/02_controlumber_theory-persistence | $ python3.7 persistence.py Please give me an integer (negative integer to quit): 999 Multiplicative loop product: 729 product: 126 product: 12 product: 2 Additive loop sum: 27 sum: 9 For the integer: 999 Additivie Persistence: 2, Additive Root: 9 Multiplicative Persistence: 4, Multiplicative Root: 2 Please give me an integer (negative integer to quit): 6 For the integer: 6 Additivie Persistence: @, Additive Root: 6 Multiplicative Persistence: , Multiplicative Root: 6 Please give me an integer (negative integer to quit): -1 joe@roland solution / ... /labs/02_controlumber_theory-persistence | $. Note that the first example demonstrates the use of "diagnostic output" (see #3 under "Getting Started"). Your final program should not print out such diagnostic output. Number Theory Additive & Multiplicative Persistence Assignment Overview The aim of this project is mostly an opportunity to work on your problem-solving skills, but it also emphasizes the use of Boolean logic and branching statements. You are going to determine the two triangular numbers which, when summed, give a square number. Background The ancient Greeks were fascinated with numbers, especially integers. They particularly were interested in the relationship between numbers and their physical realization. That is, numbers were very concrete to the Greeks, as they often talked and represented them in physical terms. Consider the relationship between numbers and two-dimensional figures, called polygonal numbers. The Greeks would arrange numbers in successive layers, called gnomons, to generate a new number related to a particular polygon. Lets look at some examples: The figure on the left is an example of "triangular" numbers, the figure on the right an example of "square" numbers. Each figure adds a gnomon, another layer, to the figure based on the shape of the figure. For each figure, the first gnomon is indicated by the green ball, the second by the red balls, the third by the yellow balls and the fourth gnomon by the blue balls. The actual triangular and square numbers are the sum of the balls in the respective figure. That is, you take the sum of all the balls in each gnomon up to the last layer you added, and that is the number. For example, the left figure represents the triangular number 10, and the right figure represents the square number 16. Below is a table of the triangular and square numbers. Take a look at those numbers, do you see any patterns? Rank (first, second, etc) Triangular Square The relationship for the square numbers should be pretty obvious. It is literally the na operation. That is, to find the nth square number, simply multiply n* n. So the 4th square number is 42, or 16. We get the term "square" from this geometric representation. For the triangular numbers it is a little less obvious, but the formula for the nth triangular number turns out to be (n2+n)/2. Thus, the 5th triangular number is (52+5)/2 which is (25+5)/2, or 15. Surprisingly, some numbers are both triangular and square numbers. Which of the above is both? A particularly interesting relationship is that any square number can be written as the sum of two triangular numbers. For example, 9 = 6 + 3. We are going to use that relationship in this project. Note that these are all integer numbers. The Greeks were interested in integers as they could work with them as if they represented real, physical objects (which to them, they did). Finally, there are many kinds of polygonal numbers. The next are pentagonal numbers (each gnomon adds a pentagon), hexagonal numbers, and so on. If you are curious, see wikipedia for more on the matter. Problem Statement So the problem is this. It is kind of a puzzle that, once solved, should end up as a rather small program. 1. Ask the user for a square number (a number which has an integer square root). 2. If the number provided is not a square, report an error and end the program. 3. If the number is a square, then find the two triangular numbers that sum to the square number (remember: there is a proof that every square number is the sum of two triangular numbers). 4. Print out the two triangular numbers and the original square number. What are the two triangular numbers which, when added together, give a square number? That's the puzzle. Once you figure out the puzzle, the program is quite short. Deliverables gnomons.py -- your solution source code Be sure to use the specified file name. Assignment Notes There are two ways to figure out the relationship between which triangular numbers sum to square numbers. Look for the pattern Look at the table of triangular and square numbers in the table. Can you find a relationship between the square numbers and the triangular numbers that sum to them? One way to help discover the relationship is to mark each square number and the triangular numbers that sum to it (highlight them, circle them, color them, etc.). Draw a picture The Greeks thought of these numbers as figures. Draw a square number figure. How can you divide the square figure into two triangular figures? Come up with a guess (hypothesis) and test it on other square number figures. Other things to think about 1. How can you figure out if a number is truly a square number? As we said, the square root should be an integer. The square root function is part of the math module. You need to import math and then use math.sqrt() . Think about how you would determine whether the result of math.sqrt() is truly an integer. The math.sqrt() always returns a float. 2. How do you determine which square a square number is? That is, is 64 the 4th square number (no), the 7th square number (no) or the 8th square number (yes). 3. If you know which square number a square number is, then if you found the pattern above you should be able to generate the triangular numbers required. Sample Run wsl. x + v - 0 X joe@tyrion - $ python3.7 gnomons.py Num: 8 8 is not a square number joe@tyrion $ python3.7 gnomons.py Num: 9 9 is a square number with a root of 3 It is the sum of the triagonal numbers 6 and 3 joe@tyrion - $ python3.7 gnomons.py Num: 289 289 is a square number with a root of 17 It is the sum of the triagonal numbers 153 and 136 joe@tyrion