Population growth modeled via differential equation: (5)

where P(t)= individuals in a population as function of time t, k= proportionality constant. Consider population growth as follows

is 0.1; the units for are 1/year.

initial time is 0 years.

final time is 40 years.

The initial population is 10 individuals.

Assume that no individuals leave the population during the time interval of interest.

1. Analytically solve this population growth problem using the techniques of calculus. just need to write Eqtn. 5 in the form and integrate both sides. Do not submit any written analysis for this task, though you will use this information for other portions of this problem.

2. solve this population growth problem using the forward Euler integration technique. Use a time step size of 2 years. Store your derivative term in an anonymous function and use that anonymous function in your forward Euler solution implementation.

3. numerically solve this population growth problem using the built-in function ode45. Instead of using a separate programmer-defined function file, however, define your function inside the ode45 function call like ode45(@(t,p) your_function, ...)

4. Finally, plot the analytic result, the forward Euler solution, and the ode45 solution on the same plot. Include an appropriate title, an appropriate -label, and label. Use different line colors and data markers for each line. Include a legend.

(sample plot looks like)

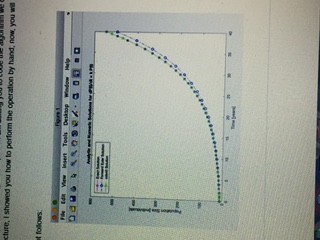
PLEASE HELP

P(t) k P(t) P(t) k P(t)