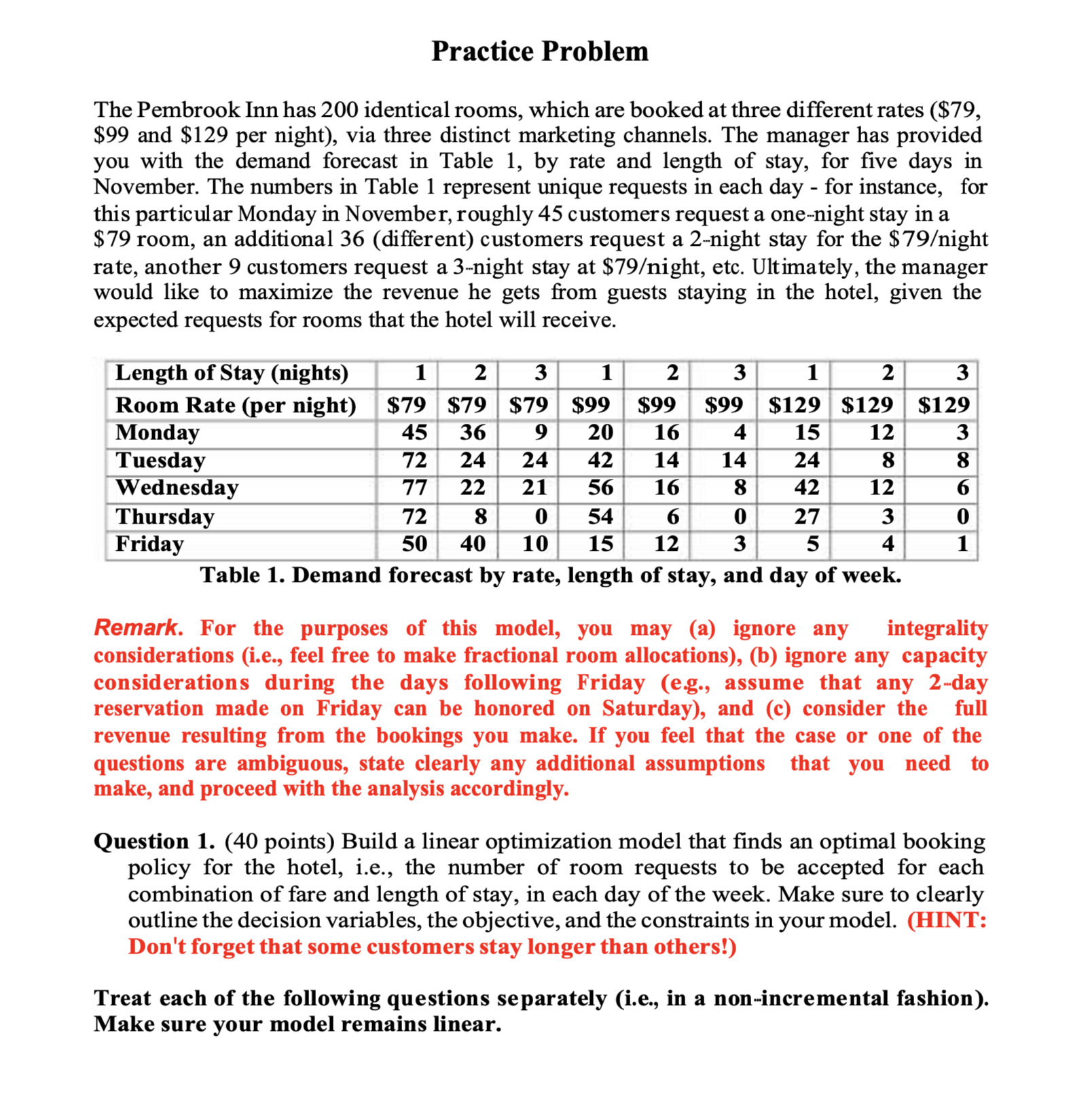
Practice Problem The Pembrook Inn has 200 identical rooms, which are booked at three different rates ($79, $99 and $129 per night), via three distinct marketing channels. The manager has provided you with the demand forecast in Table 1, by rate and length of stay, for five days in November. The numbers in Table 1 represent unique requests in each day - for instance, for this particular Monday in November, roughly 45 customers request a one-night stay in a $79 room, an additional 36 (different) customers request a 2-night stay for the $79/night rate, another 9 customers request a 3-night stay at $79/night, etc. Ultimately, the manager would like to maximize the revenue he gets from guests staying in the hotel, given the expected requests for rooms that the hotel will receive. Length of Stay (nights) Room Rate (per night) 1 2 $79 $79 $79 $99 3 1 2 3 1 2 3 $99 $99 $129 $129 $129 Monday 45 36 9 20 16 4 15 12 3 Tuesday 72 24 24 42 14 14 24 8 8 Wednesday 77 22 21 56 16 8 42 12 6 Thursday 72 8 0 54 6 0 27 3 0 Friday 50 40 10 15 12 3 5 4 1 Table 1. Demand forecast by rate, length of stay, and day of week. integrality Remark. For the purposes of this model, you may (a) ignore any considerations (i.e., feel free to make fractional room allocations), (b) ignore any capacity considerations during the days following Friday (e.g., assume that any 2-day reservation made on Friday can be honored on Saturday), and (c) consider the full revenue resulting from the bookings you make. If you feel that the case or one of the questions are ambiguous, state clearly any additional assumptions that you need to make, and proceed with the analysis accordingly. Question 1. (40 points) Build a linear optimization model that finds an optimal booking policy for the hotel, i.e., the number of room requests to be accepted for each combination of fare and length of stay, in each day of the week. Make sure to clearly outline the decision variables, the objective, and the constraints in your model. (HINT: Don't forget that some customers stay longer than others!) Treat each of the following questions separately (i.e., in a non-incremental fashion). Make sure your model remains linear.