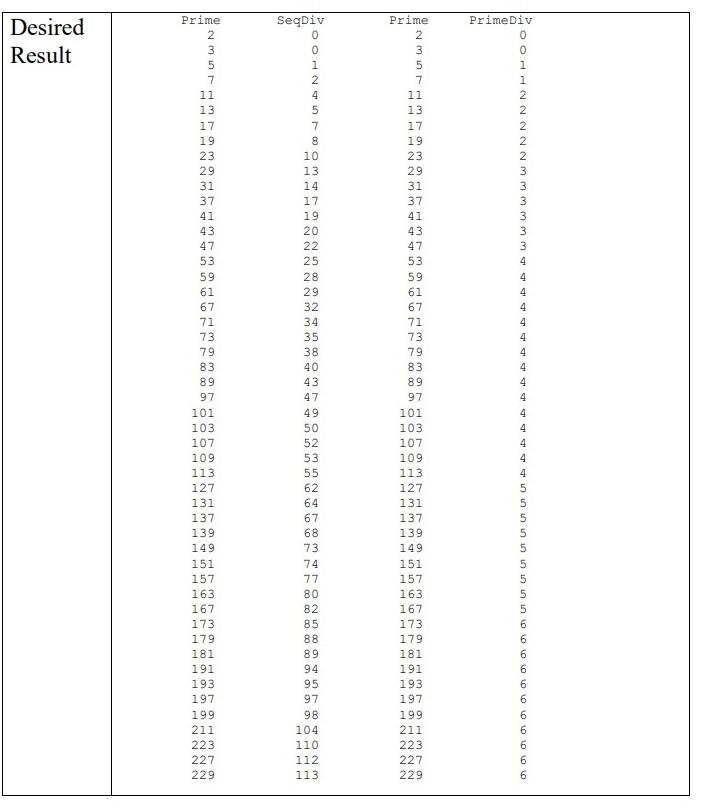
Prime Numbers Lab Exercise This lab exercise involves enhancing a (partially) working program. The "starter code" finds the first 50 prime numbers and keeps a count of how many divisors were tested in order to determine whether each number is really a prime. The assignment is to implement another, slightly different, algorithm for finding prime numbers, and keep a count of how many divisors are tested in order to determine whether or not each number is a prime. The starter code also includes a method named "outputResults" which will display the results of both algorithms, side-by-side on the screen. Inefficient Prime Number Generator: Sequential Divisors The method named primes SequentialDivisors determines whether a number n is prime by checking whether 2, 3, 4, 5, 6, ..., n/2 is a divisor with no remainder. If such a divisor is found, then n is NOT a prime. (That is, if the integer division n/ divisor has remainder=0, then n is NOT a prime number.) This code stores each prime number along with the number of divisor values which were checked in order to determine that the number is a prime. These are stored in a two-dimensional array for later display. The divisorCount variable is really a count of how many times the if (number divisor == 0) instruction was executed in order to determine that the number is indeed a prime number. A More Efficient Prime Number Generator: Prime Divisors A more efficient approach is to check whether any of the prime numbers less than or equal to the square root of n can divide n evenly (with remainder-0). If not, then n is a prime number. To understand this, consider a few examples: There is no point in testing for divisibility by 9 when the program has already checked for divisibility by 3. There is no point in testing for divisibility by 15 when the program has already checked for divisibility by 5. There are actually two advantages which this algorithm has over the first: The new algorithm is using only proven prime numbers as the test divisors, rather than all numbers >= 2 as test divisors. This approach avoids unnecessary passes through the loop. The new algorithm also takes advantage of the fact that we do not need to test divisors up to half of the candidate prime number; instead, testing divisors up to the square root of the candidate prime number is enough. Programming Exercise Implement the code for the primesPrimeDivisors method, so that it stores the first 50 prime numbers in the array, using the improved approach described above. You will need to store the prime numbers in the array, but use the prime numbers which are already in the array as the test divisors of the new "candidate" numbers. Also store in the array the divisor count of how many divisor values must be checked to determine whether each candidate is a prime. The output for the starter code (Primes Comparison.java) is shown on page 3 of this document. This illustrates that the improved algorithm has not been completed, because the two columns on the right side contain only zeroes. The expected output for the completed program is shown on page 4 of this document. HINT: First, copy the code from primesSequential Divisors into primes PrimeDivisors, and change the copied code so that it uses the array contents as the divisor values. . Second, change the loop continuation condition to check for the square root of n, rather than n/2. (In the end, the primesSequentialDivisors and primesPrimeDivisors methods are very similar, but not identical.) Sample Output The next two pages of this document contain sample output of the initial ("starter code") program, as well as the expected output from the finished algorithm. Initial (Starter Code) Output Prime gumurH 2 W W NNHHHH 3. 5 7 11 13 17 19 23 29 31 37 41 43 47 53 0 10 10 in 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 SeqDiv 0 - PWPNOW NOWwo U NN O UND WOUNHOO 1 2 5 7 8 10 DAAD NNNNNH 4 13 14 17 19 20 22 25 28 29 32 34 35 38 40 43 47 49 50 i i u o o worr 52 53 55 62 64 67 68 73 00 / 74 77 80 O o o o 00 00 00 00 82 N 85 88 0 89 94 o 95 - 97 86 0 104 110 112 113 HHHO WNOP Prime 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 PrimeDiv 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Desired Result Prime 23573 11 13 17 19 SWW NNH 23 ama 29 31 37 ma 41 43 47 53 59 61 10 10 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 SeqDiv 0 DUAN 600 GNO6 JAWOL GANHOO HANNNNN m m m m 0 1 2 4 5 7 10 8 13 14 17 19 20 22 25 28 29 32 34 35 00 00 38 40 43 47 49 50 W NO 52 53 55 62 64 67 68 73 74 77 80 82 85 100 88 89 94 95 97 98 104 110 112 113 Prime 23573 11 13 17 19 GG WWWNHOOO060 00 00 LLLAAA W W N NH 23 939 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 M in 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 PrimeDiv 0 OOHHNN NN N m m m m m ma 0 1 1 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 5 in ininin in in in in 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6