Answered step by step
Verified Expert Solution
Question
1 Approved Answer
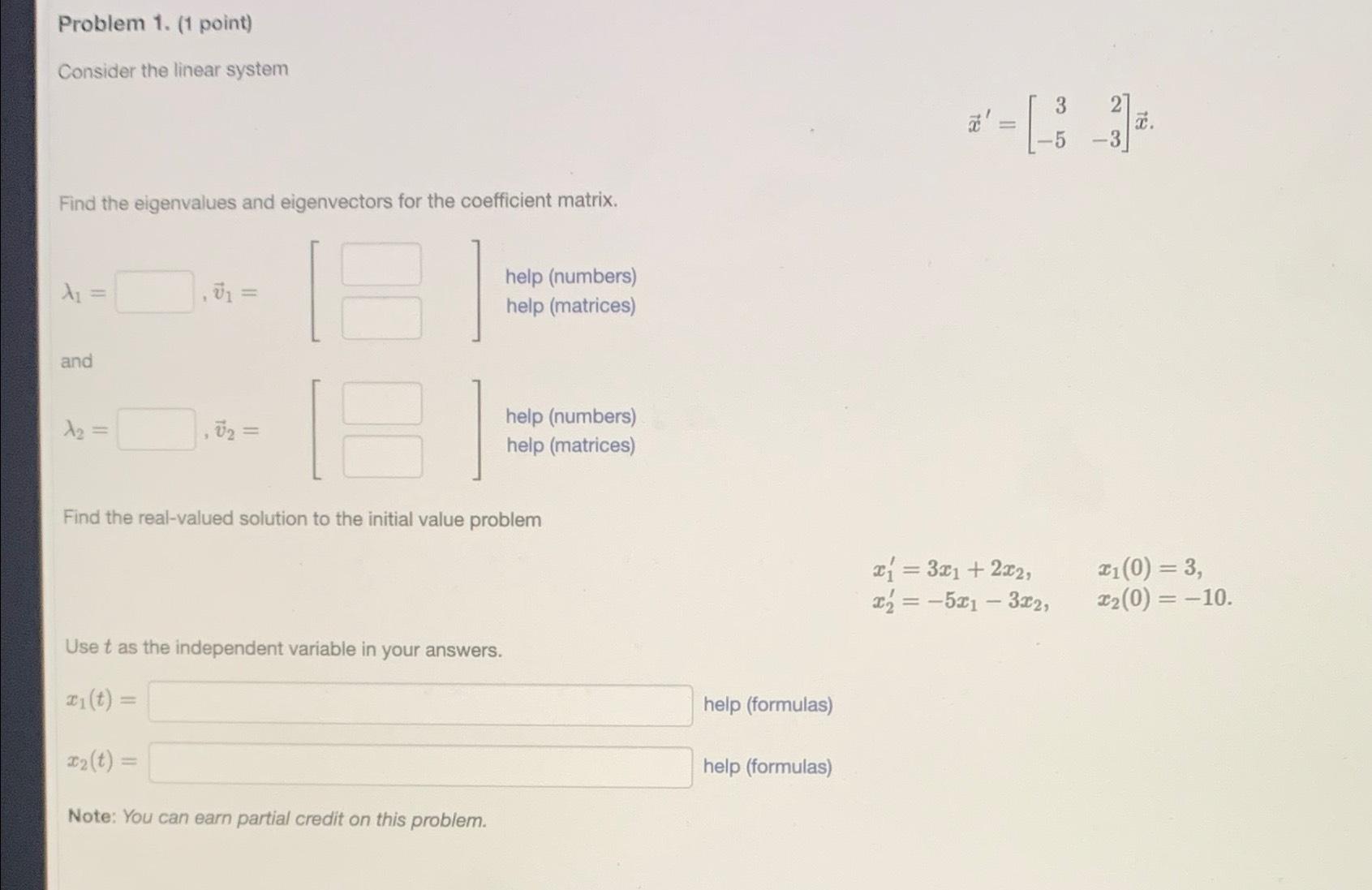
Problem 1. (1 point) Consider the linear system vec(x)^(')=[[3,2],[-5,-3]]vec(x) Find the eigenvalues and eigenvectors for the coefficient matrix. lambda _(1)=,vec(v)_(1)=,[,]{(:[ help (numbers) ]),( help
Problem 1. (1 point)\ Consider the linear system\
vec(x)^(')=[[3,2],[-5,-3]]vec(x)\ Find the eigenvalues and eigenvectors for the coefficient matrix.\
\\\\lambda _(1)=,vec(v)_(1)=,[,]{(:[ help (numbers) ]),( help (matrices) ):}\ and\
\\\\lambda _(2)=,vec(v)_(2)=,[,]{(:[]),( help (numbers) ),( help (matrices) ):}\ Find the real-valued solution to the initial value problem\
x_(1)^(')=3x_(1)+2x_(2),x_(1)(0)=3\ x_(2)^(')=-5x_(1)-3x_(2),x_(2)(0)=-10\ Use
tas the independent variable in your answers.\
x_(1)(t)= elp (formulas) \ x_(2)(t)= help (formulas) \ Note: You can earn partial credit on this problem.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


