
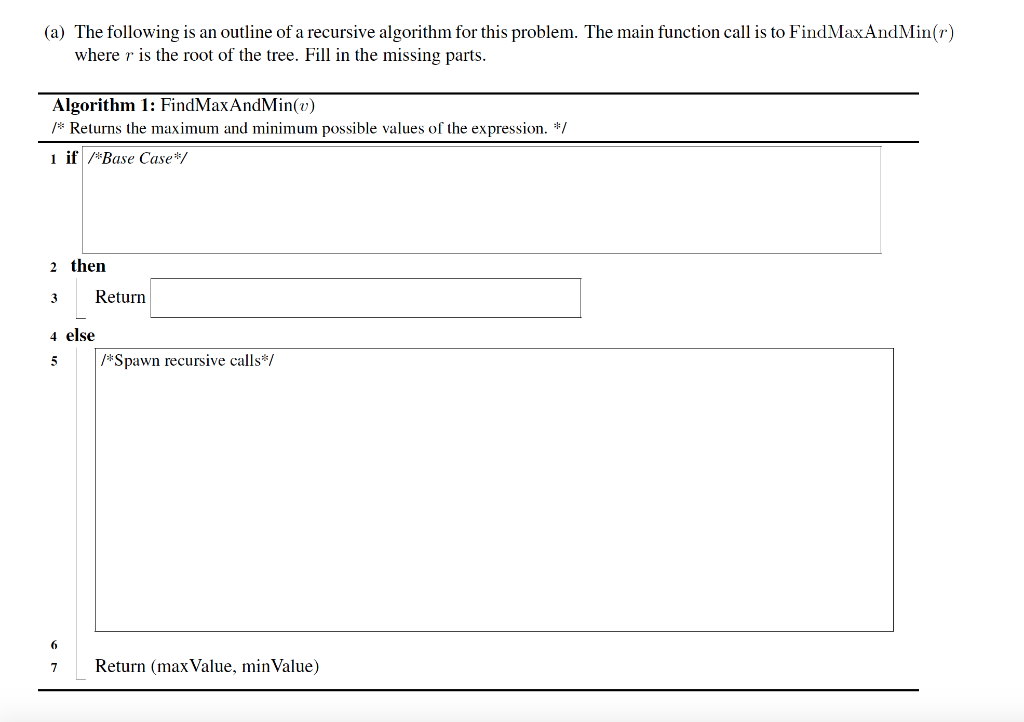
Problem 1 [30 points] Assume that you are given a fully parenthesized numerical expression with positive and negative numbers and like the following (1+3] + (1+1] + [7)) + ((18] + (-3)) + ([+1] [+4))) where the only possible operations between two numbers are addition + and subtraction Notice that to avoid confusion we use brackets, e.g., [-7] to denote a number together with its sign. Now consider the same expression with the operators + and missing, i.e, replaced by ? (1+3] ? ([+1] ? [+71) ) ? ( [+8] ? [-3) ? ([+1] ? [+4)) Your goal is figure out the maximum and minimum possible value of the expression when ? are replaced with either + or -. For example, to maximize the above expression we have replace the ? as follows ([+3] 1+ (+1] [7) ) ((18] + [-3)) ((+1] + [+4)) ) = 27. On the other hand to minimize it we have to replace them as (1+3] ((+1) (+7)) ) + ((18] + (-3)) ((+1] +(+41)) = -21. In general you will be given an arithmetic expression with n numbers structured as a binary tree with root r where the leaves correspond to the numbers. For example, the input may be the following tree corresponding to the expression + above: +3 +1 -8 -3 +4 In this case, the output of your algorithm should be (27, -21). (a) The following is an outline of a recursive algorithm for this problem. The main function call is to FindMaxAndMin(r) where r is the root of the tree. Fill in the missing parts. Algorithm 1: FindMaxAndMin() /* Returns the maximum and minimum possible values of the expression. */ 1 if /*Base Case*/ 2 then 3 Return 4 else 5 /*Spawn recursive calls/ 6 7 Return (max Value, min Value) Problem 1 [30 points] Assume that you are given a fully parenthesized numerical expression with positive and negative numbers and like the following (1+3] + (1+1] + [7)) + ((18] + (-3)) + ([+1] [+4))) where the only possible operations between two numbers are addition + and subtraction Notice that to avoid confusion we use brackets, e.g., [-7] to denote a number together with its sign. Now consider the same expression with the operators + and missing, i.e, replaced by ? (1+3] ? ([+1] ? [+71) ) ? ( [+8] ? [-3) ? ([+1] ? [+4)) Your goal is figure out the maximum and minimum possible value of the expression when ? are replaced with either + or -. For example, to maximize the above expression we have replace the ? as follows ([+3] 1+ (+1] [7) ) ((18] + [-3)) ((+1] + [+4)) ) = 27. On the other hand to minimize it we have to replace them as (1+3] ((+1) (+7)) ) + ((18] + (-3)) ((+1] +(+41)) = -21. In general you will be given an arithmetic expression with n numbers structured as a binary tree with root r where the leaves correspond to the numbers. For example, the input may be the following tree corresponding to the expression + above: +3 +1 -8 -3 +4 In this case, the output of your algorithm should be (27, -21). (a) The following is an outline of a recursive algorithm for this problem. The main function call is to FindMaxAndMin(r) where r is the root of the tree. Fill in the missing parts. Algorithm 1: FindMaxAndMin() /* Returns the maximum and minimum possible values of the expression. */ 1 if /*Base Case*/ 2 then 3 Return 4 else 5 /*Spawn recursive calls/ 6 7 Return (max Value, min Value)








