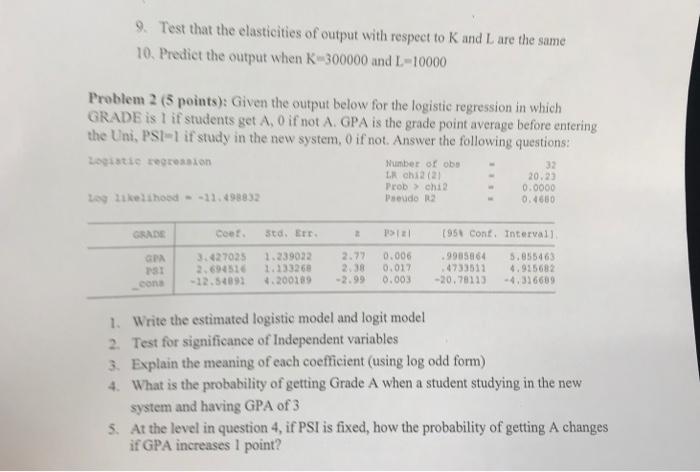
Problem 1 (5 points): Given the output below where Loutput, LK and LL are the logarithm of respective variables. Use a=0.05 to answer the questions Source SS MS Model Residual 2.64225721 .334266431 2 17 1.32112861 019662731 Number of cbs F12, 171 Prob > F R-squared Ady R-squared Root MSE 20 67.19 0.0000 0.8877 0.8745 14022 Total 2.97652364 19 156659139 = Loutput Coef. Std. Err. P>iti 1956 Conf. Intervall LK LL cons . 9730341 .0438198 -.5423927 .2560507 -5059589 1.975104 3.80 0.09 -0.27 0.001 0.932 0.787 .4328144 -1.02366 -4.709498 1.513254 1.1113 3.624712 Covariance matrix of coefficients of regress model e (V) LK LL cons LK LL cons .06556194 -. 12207138 .30476326 25599436 -.83444655 3.9010354 1. Write down the population function and sample function. 2. Explain the meaning of the estimated coefficients. 3. Are these coefficients as your expectation? 4. What is the meaning of the sum of two slope coefficients? 5. What is R, explain for its meaning? 6. Test for the significance of each independent variable. 7. Test for the overall significance of the model? 8. Test that production function is constant returns to scale. 9. Test that the elasticities of output with respect to K and I are the same 10. Predict the output when K 300000 and L-10000 Problem 2 (5 points): Given the output below for the logistic regression in which GRADE is 1 if students get A. O if not A. GPA is the grade point average before entering the Uni, PST-1 if study in the new system, 0 if not. Answer the following questions: Listie regression Number of obe 20.23 LA chi2 (21 Prob > chi Pseudo R Likelihood -11.498832 0.0000 0.4680 Coet Std. Er 151 1951 Cont. Intervall 1 cona 3.427025 2.69451 -12.5409 1.239022 1.133260 1.200109 2.72 2.38 -2.99 0.000 0.017 0.003 .9985864 4733511 -20.78113 5.855463 4.915682 -4.316689 1. Write the estimated logistic model and logit model 2. Test for significance of Independent variables 3. Explain the meaning of each coefficient (using log odd form) 4. What is the probability of getting Grade A when a student studying in the new system and having GPA of 3 5. At the level in question 4, if PSI is fixed, how the probability of getting A changes if GPA increases I point? Problem 1 (5 points): Given the output below where Loutput, LK and LL are the logarithm of respective variables. Use a=0.05 to answer the questions Source SS MS Model Residual 2.64225721 .334266431 2 17 1.32112861 019662731 Number of cbs F12, 171 Prob > F R-squared Ady R-squared Root MSE 20 67.19 0.0000 0.8877 0.8745 14022 Total 2.97652364 19 156659139 = Loutput Coef. Std. Err. P>iti 1956 Conf. Intervall LK LL cons . 9730341 .0438198 -.5423927 .2560507 -5059589 1.975104 3.80 0.09 -0.27 0.001 0.932 0.787 .4328144 -1.02366 -4.709498 1.513254 1.1113 3.624712 Covariance matrix of coefficients of regress model e (V) LK LL cons LK LL cons .06556194 -. 12207138 .30476326 25599436 -.83444655 3.9010354 1. Write down the population function and sample function. 2. Explain the meaning of the estimated coefficients. 3. Are these coefficients as your expectation? 4. What is the meaning of the sum of two slope coefficients? 5. What is R, explain for its meaning? 6. Test for the significance of each independent variable. 7. Test for the overall significance of the model? 8. Test that production function is constant returns to scale. 9. Test that the elasticities of output with respect to K and I are the same 10. Predict the output when K 300000 and L-10000 Problem 2 (5 points): Given the output below for the logistic regression in which GRADE is 1 if students get A. O if not A. GPA is the grade point average before entering the Uni, PST-1 if study in the new system, 0 if not. Answer the following questions: Listie regression Number of obe 20.23 LA chi2 (21 Prob > chi Pseudo R Likelihood -11.498832 0.0000 0.4680 Coet Std. Er 151 1951 Cont. Intervall 1 cona 3.427025 2.69451 -12.5409 1.239022 1.133260 1.200109 2.72 2.38 -2.99 0.000 0.017 0.003 .9985864 4733511 -20.78113 5.855463 4.915682 -4.316689 1. Write the estimated logistic model and logit model 2. Test for significance of Independent variables 3. Explain the meaning of each coefficient (using log odd form) 4. What is the probability of getting Grade A when a student studying in the new system and having GPA of 3 5. At the level in question 4, if PSI is fixed, how the probability of getting A changes if GPA increases I point