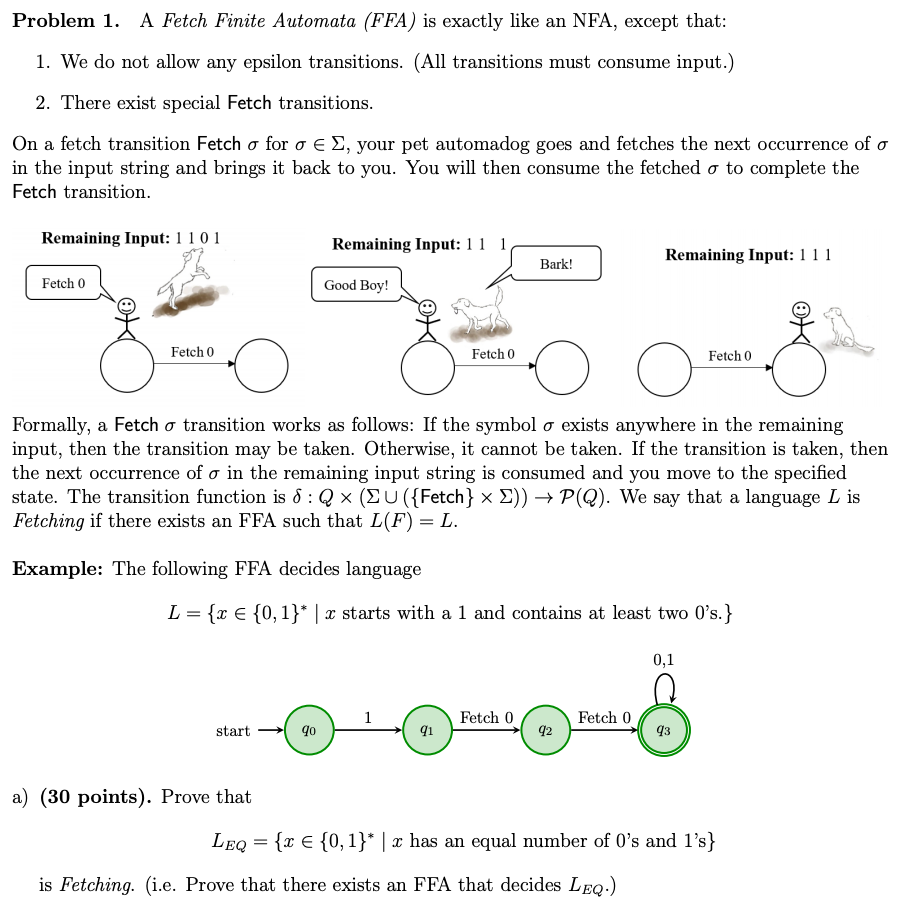
Problem 1. A Fetch Finite Automata (FFA) is exactly like an NFA, except that: 1. We do not allow any epsilon transitions. (All transitions must consume input.) 2. There exist special Fetch transitions. On a fetch transition Fetch o for o e, your pet automadog goes and fetches the next occurrence of o in the input string and brings it back to you. You will then consume the fetched o to complete the Fetch transition. Remaining Input: 1101 Remaining Input: 11 1 Remaining Input: 111 Bark! Fetch 0 Good Boy! Fetch 0 Fetch 0 Fetch 0 Formally, a Fetch o transition works as follows: If the symbol o exists anywhere in the remaining input, then the transition may be taken. Otherwise, it cannot be taken. If the transition is taken, then the next occurrence of o in the remaining input string is consumed and you move to the specified state. The transition function is 8: Q (EU({Fetch} )) + P(Q). We say that a language L is Fetching if there exists an FFA such that L(F) = L. Example: The following FFA decides language L = {x {0,1}* . x starts with a 1 and contains at least two 0's.} 0,1 Fetch 0 Fetch 0 start 90 91 92 93 a) (30 points). Prove that LEQ = {2 {0,1}* | x has an equal number of O's and ls} is Fetching. (i.e. Prove that there exists an FFA that decides LEQ.) Definition 1 (Permutation). A permutation of the string r is a string formed by reordering the elements of x. For example, if x = 0012, then 1020 is a permutation of x. The set S of permutations of x = 0012 is S = {0012, 0021, 0102, 0201, 1002, 2001, 0120, 0210, 1020, 2010, 1200, 2100}. b) (20 points). Consider the following FFA F: 1 2 start qo 91 92 93 94 Fetch 0 String x = 122211000 is in L(F). Write three distinct permutations of x (other than u itself) that are also in L(F). c) (50 points). Prove the following pumping lemma about Fetching languages: Lemma 1. For all Fetching languages L, there exists an neN such that for all x E L with 21 > n, there erist strings a,b,c such that w = abc e L where w is a permutation of r and i. 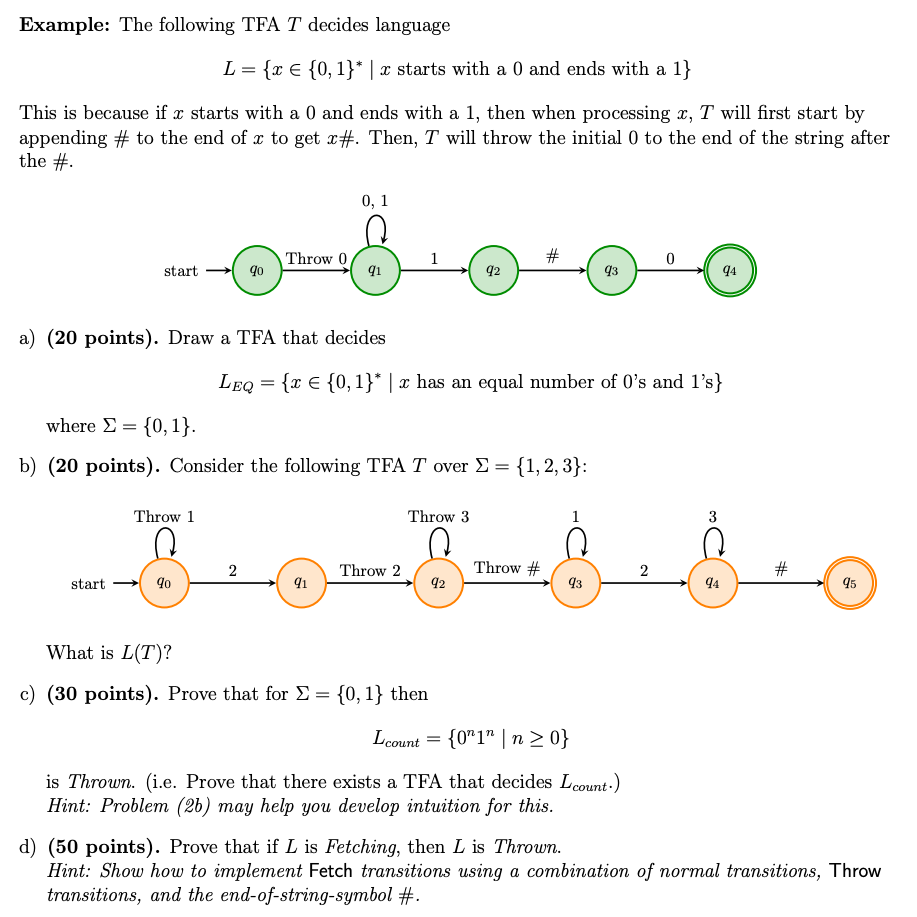ab 0 iii. Vi > 0, ab'c EL Hint: Part (16) should help you develop intuition for this. d) (30 points). Use Lemma 1 from (1c) to prove that Lcount = {0"1" | n>0} is not Fetching. Problem 2. A Throwable Finite Automata (TFA) is exactly like an NFA, except that: 1. Before processing the string, the TFA appends a special end-of-string-symbol # to the end of the string. Recall here that is the input alphabet of the TFA. 2. There exist special Throw transitions. On input re S*, the TFA will append # to the input I and operate on the string x# as an NFA would operate (but with Throw transitions). From now on, we will refer to the string x# as the input" string and E# = EU{#} as the "input alphabet, and will refer to x as the "original input string and as the "original input alphabet. Please take note that there are no # symbols in any original input string 2 (e.g. I = 0#11 is not allowed) On a throw transition Throw o for o E E#, if your next input symbol is o, you can throw it to the end of the input string. Remaining Input: 1 2 3 # Remaining Input: 2 3 # . Remaining Input: 2 3 # 1 2 Throw 1 Throw 1 Throw 1 O o o Formally, a Throw o transition works as follows: If your next input symbol is o, then the transition may be taken. Otherwise, it may not be taken. If the transition is taken, you move the input symbol o from the beginning of the remaining input string to the end of the string and move to the specified state. The transition function is therefore 8: Q (E# U{e} U ({Throw} * E#)) + P(Q). We say that a TFA T accepts an "original input string r if there exists at least one computation path in T on input c# that halts in an accepting state. Note that if a computation path continues forever (which could occur if you loop and continuously throw symbols in the input string, so that you never run out of input), then that computation path is not considered accepting. We say that a language L is Thrown if there exists a TFA such that L(T) = L. Note that the language of T is the set of "original input" strings that are accepted. Thus, L(T) will never contain a string that contains a #. Example: The following TFA T decides language L = {x {0,1}* | x starts with a 0 and ends with a 1} This is because if x starts with a 0 and ends with a 1, then when processing x, T will first start by appending # to the end of x to get #. Then, T will throw the initial 0 to the end of the string after the # 0,1 Throw 0 # 0 start 90 91 92 23 94 a) (20 points). Draw a TFA that decides LEQ = {0 {0,1}* | x has an equal number of O's and ls} where 2 = {0,1}. b) (20 points). Consider the following TFA T over = {1, 2, 3}: Throw 1 Throw 3 1 3 2 Throw 2 Throw # 2 # start 90 91 92 93 94 95 What is L(T)? c) (30 points). Prove that for = {0,1} then Lcount = {0"1" | n>0} is Thrown. (i.e. Prove that there exists a TFA that decides Lcount.) Hint: Problem (26) may help you develop intuition for this. d) (50 points). Prove that if L is Fetching, then L is Thrown. Hint: Show how to implement Fetch transitions using a combination of normal transitions, Throw transitions, and the end-of-string-symbol #. Problem 1. A Fetch Finite Automata (FFA) is exactly like an NFA, except that: 1. We do not allow any epsilon transitions. (All transitions must consume input.) 2. There exist special Fetch transitions. On a fetch transition Fetch o for o e, your pet automadog goes and fetches the next occurrence of o in the input string and brings it back to you. You will then consume the fetched o to complete the Fetch transition. Remaining Input: 1101 Remaining Input: 11 1 Remaining Input: 111 Bark! Fetch 0 Good Boy! Fetch 0 Fetch 0 Fetch 0 Formally, a Fetch o transition works as follows: If the symbol o exists anywhere in the remaining input, then the transition may be taken. Otherwise, it cannot be taken. If the transition is taken, then the next occurrence of o in the remaining input string is consumed and you move to the specified state. The transition function is 8: Q (EU({Fetch} )) + P(Q). We say that a language L is Fetching if there exists an FFA such that L(F) = L. Example: The following FFA decides language L = {x {0,1}* . x starts with a 1 and contains at least two 0's.} 0,1 Fetch 0 Fetch 0 start 90 91 92 93 a) (30 points). Prove that LEQ = {2 {0,1}* | x has an equal number of O's and ls} is Fetching. (i.e. Prove that there exists an FFA that decides LEQ.) Definition 1 (Permutation). A permutation of the string r is a string formed by reordering the elements of x. For example, if x = 0012, then 1020 is a permutation of x. The set S of permutations of x = 0012 is S = {0012, 0021, 0102, 0201, 1002, 2001, 0120, 0210, 1020, 2010, 1200, 2100}. b) (20 points). Consider the following FFA F: 1 2 start qo 91 92 93 94 Fetch 0 String x = 122211000 is in L(F). Write three distinct permutations of x (other than u itself) that are also in L(F). c) (50 points). Prove the following pumping lemma about Fetching languages: Lemma 1. For all Fetching languages L, there exists an neN such that for all x E L with 21 > n, there erist strings a,b,c such that w = abc e L where w is a permutation of r and i. ab 0 iii. Vi > 0, ab'c EL Hint: Part (16) should help you develop intuition for this. d) (30 points). Use Lemma 1 from (1c) to prove that Lcount = {0"1" | n>0} is not Fetching. Problem 2. A Throwable Finite Automata (TFA) is exactly like an NFA, except that: 1. Before processing the string, the TFA appends a special end-of-string-symbol # to the end of the string. Recall here that is the input alphabet of the TFA. 2. There exist special Throw transitions. On input re S*, the TFA will append # to the input I and operate on the string x# as an NFA would operate (but with Throw transitions). From now on, we will refer to the string x# as the input" string and E# = EU{#} as the "input alphabet, and will refer to x as the "original input string and as the "original input alphabet. Please take note that there are no # symbols in any original input string 2 (e.g. I = 0#11 is not allowed) On a throw transition Throw o for o E E#, if your next input symbol is o, you can throw it to the end of the input string. Remaining Input: 1 2 3 # Remaining Input: 2 3 # . Remaining Input: 2 3 # 1 2 Throw 1 Throw 1 Throw 1 O o o Formally, a Throw o transition works as follows: If your next input symbol is o, then the transition may be taken. Otherwise, it may not be taken. If the transition is taken, you move the input symbol o from the beginning of the remaining input string to the end of the string and move to the specified state. The transition function is therefore 8: Q (E# U{e} U ({Throw} * E#)) + P(Q). We say that a TFA T accepts an "original input string r if there exists at least one computation path in T on input c# that halts in an accepting state. Note that if a computation path continues forever (which could occur if you loop and continuously throw symbols in the input string, so that you never run out of input), then that computation path is not considered accepting. We say that a language L is Thrown if there exists a TFA such that L(T) = L. Note that the language of T is the set of "original input" strings that are accepted. Thus, L(T) will never contain a string that contains a #. Example: The following TFA T decides language L = {x {0,1}* | x starts with a 0 and ends with a 1} This is because if x starts with a 0 and ends with a 1, then when processing x, T will first start by appending # to the end of x to get #. Then, T will throw the initial 0 to the end of the string after the # 0,1 Throw 0 # 0 start 90 91 92 23 94 a) (20 points). Draw a TFA that decides LEQ = {0 {0,1}* | x has an equal number of O's and ls} where 2 = {0,1}. b) (20 points). Consider the following TFA T over = {1, 2, 3}: Throw 1 Throw 3 1 3 2 Throw 2 Throw # 2 # start 90 91 92 93 94 95 What is L(T)? c) (30 points). Prove that for = {0,1} then Lcount = {0"1" | n>0} is Thrown. (i.e. Prove that there exists a TFA that decides Lcount.) Hint: Problem (26) may help you develop intuition for this. d) (50 points). Prove that if L is Fetching, then L is Thrown. Hint: Show how to implement Fetch transitions using a combination of normal transitions, Throw transitions, and the end-of-string-symbol #<><>