Problem 1: Climate change in the coastal ocean (25 points)

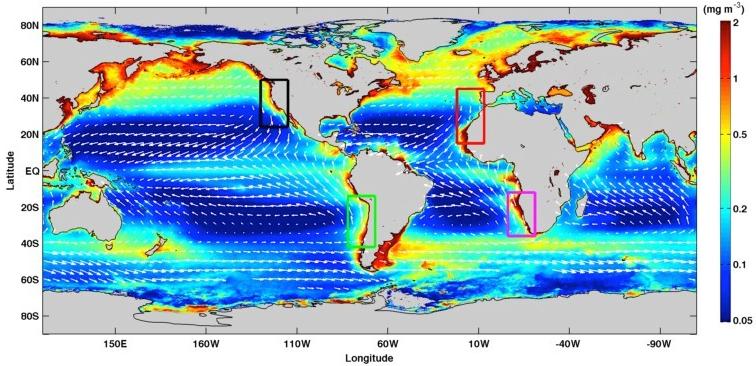
Global climate change is expected to have large impacts on the coastal ocean. This is particularly true in Eastern Boundary Current Systems (EBCS), which are located on the eastern margins of major ocean basins around the world (see map above: California in black, Canary in red, Humboldt in green and Benguela in pink). These EBCS benefit from coastal upwelling currents (measured in units of m2/s), which promote the productivity of fisheries by bringing cold and nutrient-rich waters to the surface where they can subsidize the base of the marine food web. Climate change is expected to alter the timing, strength and persistence of these upwelling currents over the course of the 21st century. In this assignment, you will analyze data from the latest generation of Earth System Models (CMIP5) used by the IPCC to determine changes in the mean and variance of

1

upwelling over time. The data consists of annual upwelling values predicted by 22 different Earth System Models for each EBCS (California, Canary, Humboldt, Benguela) from 1950 to 2099.

Begin by downloading each dataset from the web
benguela <- read.csv("http://faraway.neu.edu/data/assn3_benguela.csv")

california <- read.csv("http://faraway.neu.edu/data/assn3_california.csv")

canary <- read.csv("http://faraway.neu.edu/data/assn3_canary.csv")

humboldt <- read.csv("http://faraway.neu.edu/data/assn3_humboldt.csv")

1. To determine whether upwelling is predicted to increase over time, you must first add a new categorical variable called period with two levels (before: 1950-2024, after: 2025-2099) to each dataset. Hint: You will need to use the function ifelse to add this variable to the dataset (4 points) 

2. For each EBCS, create a new data frame containing the following three variables (columns): year, period, and the multimodel mean. The multimodel mean is simply the average up- welling value across all 22 Earth System Models. Hint: Function rowMeans will be useful for answering this question (4 points) 

3. We are now ready to determine whether the multimodel mean of upwelling differs between the before vs. after periods. Before proceeding with the test, check whether the distribution of the data is normal for each period and EBCS using the appropriate diagnostic test. If the data in any period or EBCS is not normal, then you will have to resort to non-parametric tests. Explain the potential consequences of using a non-parametric instead of a parametric test (4 points) 

4. Given your answer to the previous question, conduct the appropriate test to compare the mul- timodel mean across periods for each EBCS. Begin by stating the null/alternate hypotheses and conclude by determining if the multimodel mean differs between periods for each EBCS (5 points) 

5. Use a grouped bar plot to show the multimodel upwelling mean averaged in the before vs. after period for each EBCS. The bars should be grouped based on EBCS (i.e., each group consists for a before and after period for an EBCS). Add error bars representing the standard error of the mean. Hint: To place the error bars in the correct x-coordinates, make sure to store the results of the barplot function barplot into a variable (e.g., bp <- barplot(...)). This variable bp will then contain the x-coordinates of each bar in the barplot (5 points) 

6. Given your statistical analyses and the figure that you produced, describe the trends in the multimodel mean upwelling over time in each EBCS (3 points) 


Problem 2: Changes in the variance (14 points)

The variance in annual upwelling is also expected to vary due to climate change, which could lead to greater year-to-year unpredictability in fisheries and stock assessments. To test for this effect, you will have to compare the variance in the before and after periods for each EBCS.

1. Begin by identifying two potential tests that could be used to determine whether the group variance differ. Make sure to also state the assumptions of each test (4 points)

1. Given your previous answer, use the appropriate diagnostic test to determine whether the group variances differ between the before and after periods in each EBCS. Begin by stating the null/alternate hypotheses and conclude by determining if the multimodel variance differs between periods for each EBCS (3 points) 

2. Use a grouped bar plot to show the multimodel upwelling variance in the before vs. after period for each EBCS. The bars should be grouped based on EBCS (3 points) 

3. Given your statistical analyses and the figure that you produced, describe the trends in the multimodel variance of upwelling over time in each EBCS. Conclude by comparing the consistency (or robustness) of the patterns in upwelling variance to that of the upwelling mean (4 points) 


Problem 3: Model consistency or congruence (11 points)

One of the major goals of climate science is to estimate uncertainty regarding climate projections in order to inform decision makers. One major source of uncertainty is model robustness or congruence, which measures the degree of agreement among projections generated by distinct Earth System Models. To determine whether this source of uncertainty is important for this dataset, you will compare the predictions of annual upwelling across all 22 Earth System Models. To do so, you will have to convert your data from the wide to the long(itudinal) format:

# Reshape data from wide to long format:

california.long <- reshape(california, varying = list(1:22),

direction = "long", timevar = "model", v.names = "upwelling")

canary.long <- reshape(canary, varying = list(1:22), direction = "long",

timevar = "model", v.names = "upwelling")

humboldt.long <- reshape(humboldt, varying = list(1:22),

direction = "long", timevar = "model", v.names = "upwelling")

benguela.long <- reshape(benguela, varying = list(1:22),

direction = "long", timevar = "model", v.names = "upwelling")

1. To measure model agreement, you decide to compare mean upwelling across all models from 1950-2099 (i.e., across both periods). What test will you run and why? Justify your answer by describing the assumptions of the test (4 points) 

2. Given your previous answer, use the appropriate test to determine whether the model means differ for each EBCS. Begin by stating the null/alternate hypotheses and conclude by deter- mining if the model means differ for each EBCS (3 points) 

3. Create a 2x2 figure where each panel represents the model means for a specific EBCS via a barplot. Do not forget to label each panel with the name of the EBCS. Describe the model differences for each EBCS and conclude about model agreement (4 points) 


BONUS: Can you identify a potential flaw in all of the analyses conducted so far? Hint: think about the assumptions of each statistical test

Latitude 80N 60N 40N 20N EQ 20S 40S 60S 80S- 150E 160W 110W 60W Longitude ALL 10W -40W -90W (mg m3) 2 1 0.5 0.2 0.1 0.05