Problem 1. Fast Matrix Power

The goal of this exercise is to modify the power method as seen in class to support Matrix Multiplication instead of integer multiplication. As an input, we are given a double array and a non-negative integer. Using recursive algorithm, given matrix M as matrix[][], and a non-negative integer k, write a method that outputs Mk . That is if k is even;

If k is odd;

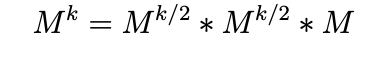
You should write your own matrix multiplication function as a subroutine. No points will be given for non-recursive or inefficient solution.

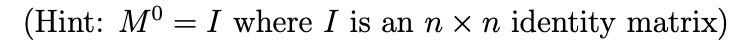
you need to use O( log k ) matrix multiplications

assume m to be square

powers method:

int powers (int a, int k) {

if (k == 0)

return 1;

int square = powers (a, k/2);

if (k%2 == 0)

return square * square;

else return square*square*a;

}

Mk = M*/2 * Mk/2 Mk = Mk/2 * Mk/2 * M (Hint: M = I where I is an n xn identity matrix) Mk = M*/2 * Mk/2 Mk = Mk/2 * Mk/2 * M (Hint: M = I where I is an n xn identity matrix)