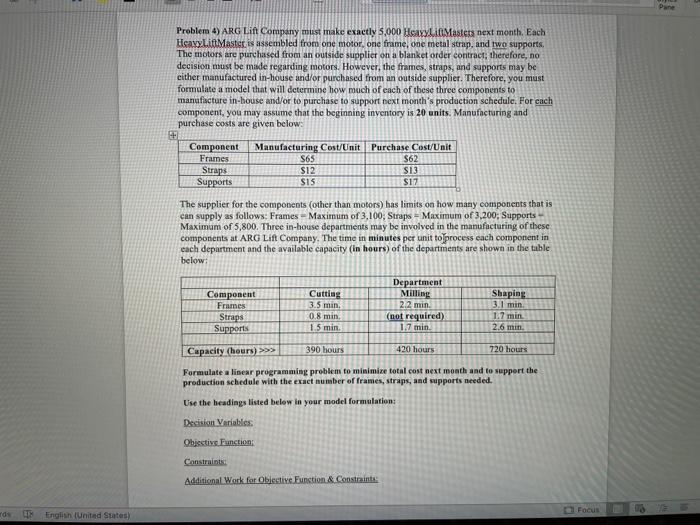
Problem 1) Kara Bee Foods adds secret natural flavorings (A, B, C, \& D) to its cheesecakes. The total amount of natural flavorings used must be at least 18 ounces per cheesecake, but not more than 24 ounces per cheesecake. At least one ounce of C must be used for each ounce of A. The amount of B used must be no more than 42% of the total amount of all natural flavorings used. The amount of D used must be at least 30% of the total amount of all natural flavorings used. The cost per ounce for the natural flavorings is $0.20 for A,$0.28 for B,$0.25 for C, and $0.30 for D. Formulate a linear programming model to minimize the total cost of the natural flavorings used in a cheesecake. Use the headings listed below in your model formulation: Decision Variables: Objective Function: Constraints: Additional Work for Objective Function \& Constraints: Problem 2) Oshkosh Beverage Company produces and sells two wine coolers (Wine Coolers A \& B). Both wine coolers are a blend of white wine, rose wine, and fruit juice; however, Wine Cooler B contains an extra ingredient - rum. Wine Cooler A: Sells for $20.00 per gallon. To meet customer taste specifications, the wibe cooler must contain the following amounts: At least 42% white wine, at least 30% rose winc, at most 55% rose wine, and exactly 25% fruit juice. Wine Cooler B: Sells for $25.00 per gallon. To meet customer taste specifications, the wine cooler must contain the following amounts: At least 22% white wine, at most 40% white winc, at least 32% rose wine, exactly 15% fruit juice, and at least 4% rum. Be careful to differentiate between the variables for Rose \& Rum. For example, because Rum is the extra ingredient, one could define Rum as follows (assuming that it is used in Wine Cooler B): EB = gallons of Extra lngredient (Rum) used in Wine Cooler B. Oshkosh Beverage purchases the white wise at $6.00 per gallon, rose wine at $5.03 per gallon, fruit juice at $2.82 per gallon, and rum at $10.00 per gallon. The supplier for the white wine can supply a maximum of 8,000 gallons. The supplier for the rose wine cas supply a maximum of 12,000 gallons. The supplier for the fruit juice can supply a maximum of 15,000 gallons. The supplier for the rum can supply a maximam of 8,000 gallons. Formulate a linear programmine to maximize profits. Hint: You will need to define 7 variables to determine the amount of each ingredient to use in each wine cooler. Use the headings listed below in your model formulation: Decision Variables: Objective Function: Constraints: Additional Work for Objective Funstion \& Coastraints: Problem 3) ABC Cheese Company produces \& sells three cheese spreads (A, B, and C) by blending two ingredients - Mild Cheddar Cheese and Spicy Cheese. These cheese spreads are packaged in 12-ounce containers (reminder: there are 16 ounces in a pound) and sold to distributors throughout the Midwest. Cheese Spread A contains 62\% Mild and 38\% Spicy. Cheese Spread B contains 52% Mild and 48% Spicy. Cheese Spread C contains 30% Mild and 70% Spicy. A dairy cooperative in Wisconsin can provide up to 11,000 pounds of Mild Cheddar Cheese for $4.20 per pound and up to 9,000 pounds of Spicy Cheese for $3.95 per pound. The cost to blend and package the cheese spreads (excluding the cost of the cheese) is $0.75 per container. Each cheese spread earns the following in revenue per container: A=$6.50,B=$7.20,C=$8.90. Formulate a linear programming problem to maximize profits next month. Carry costs and coefficients out to 2 decimals. Use the headings listed below in your model formulation: Decision Variables: Cheese Spread A: Cheese Spread B: Cheese Spread C: Objective Function: Constraints: Additional Work for Objective Function \& Constraints: Problem 4) ARG Lift Company must make exactly 5,000 HelvylifiMastets next month. Each Hemyyliftulaster, is assembled from one motor, one frame, ooc metal surap, and rwo supports. The motors are purchased from an outside supplict on a blanket order contract; therefore, no decision must be made regarding motors. However, the fimes, straps, and supports may be cither manufactured in-house and/or purchased from an outside supplier. Therefore, you must formulate a model that will determine how mach of each of these three components to manuficture in-house and/or to purchase to support next month's prodaction schedule. For each component, you may assume that the beginning inyentory is 20 anits. Manufacturing and purchase costs are given below: The supplier for the components (other than motors) bas limits on how many components that is can supply as follows: Frames - Maximum of 3,100; Straps = Maximum of 3,200; Supports Maximum of 5,800 . Three in-house departments may be involved in the manufacturing of these. components at ARG Lift Company. The time in minutes per unit tolprocess each compponent in each department and the available capacity (in hours) of the departments are showa in the table below: Formulate a linear programmiag problem to miaimixe total cost next moath and to seppert the production schedule with the exact number of frames, straps, and supports needed. Use the headiags listed below in your model formulation: Decision Variabiss. Qbiestive Function: Constraintst Additional Work far Objective Funstion & Constrainte