Let us consider a two-link robotic device as a double pendulum undergoing 2-D motion in a gravity field g. The coordinates θ₁ and θ₂ describe the orientation of the bars, with θ₁ and θ₂ being positive for counterclockwise rotations from vertical. Use Lagrange's method to find the EOM's of the system using the generalized coordinates of θ₁ and θ₂.

 

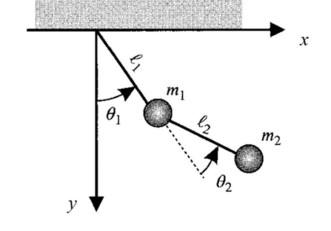
In this problem, you might need to use the following formula to simplify the calculation:

 

cos(α-β) = sin α sin β+ cos α cos β

 

Problem 1a) Based on the configuration of the system, determine the number of the degree-of-freedom (DOF).

Problem 1b) The origin of this robotic system is set to be located at the top-left point. The coordinate of the x- and y-directions are shown as the figure. What are the generalized kinematic equations of m₁ and m₂?

Problem 1c) To synthesize the dynamic equations using Lagrange's method, which of the following equation needs to be used before the partial differential process? Select all that applies.

Problem 1d) What is the kinetic energy of the system based on your kinematic equations?

Problem 1e) What is the potential energy of such a system?

Problem 1f) Which of the following operation is a required procedure to derive the dynamic equation of the i^th component by using Lagrange's method?

Problem 1g) Based on the problem statement, what are the external force applied to the masses m₁ and m₂, individually? Fill in the blanks.

Problem 1h) Based on the setup of this system, how many dynamic equations should be derived for this robotic system?

Problem 1i) What is the work created by external forces?

Problem 1j) Which of the following equations are the dynamic equations of this robotic system based on the derivation from 1(a) to 1(i)? Check all that applies.

Transcribed Image Text:

0₁ m 02 11 2 r 0₁ m 02 11 2 r

Answer rating: 100% (QA)

Problem 1a The system has two links that can rotate around their respective joints so there are two degrees of freedom DOF in this system Problem 1b T... View the full answer