Problem 21-07 (Part Level Submission)
Nash Inc. manufactures an X-ray machine with an estimated life of 12 years and leases it to Chambers Medical Center for a period of 10 years. The normal selling price of the machine is $480,948, and its guaranteed residual value at the end of the non-cancelable lease term is estimated to be $16,100. The hospital will pay rents of $58,100 at the beginning of each year. Nash incurred costs of $233,000 in manufacturing the machine and $12,600 in legal fees directly related to the signing of the lease. Nash has determined that the collectibility of the lease payments is probable and that the implicit interest rate is 5%.
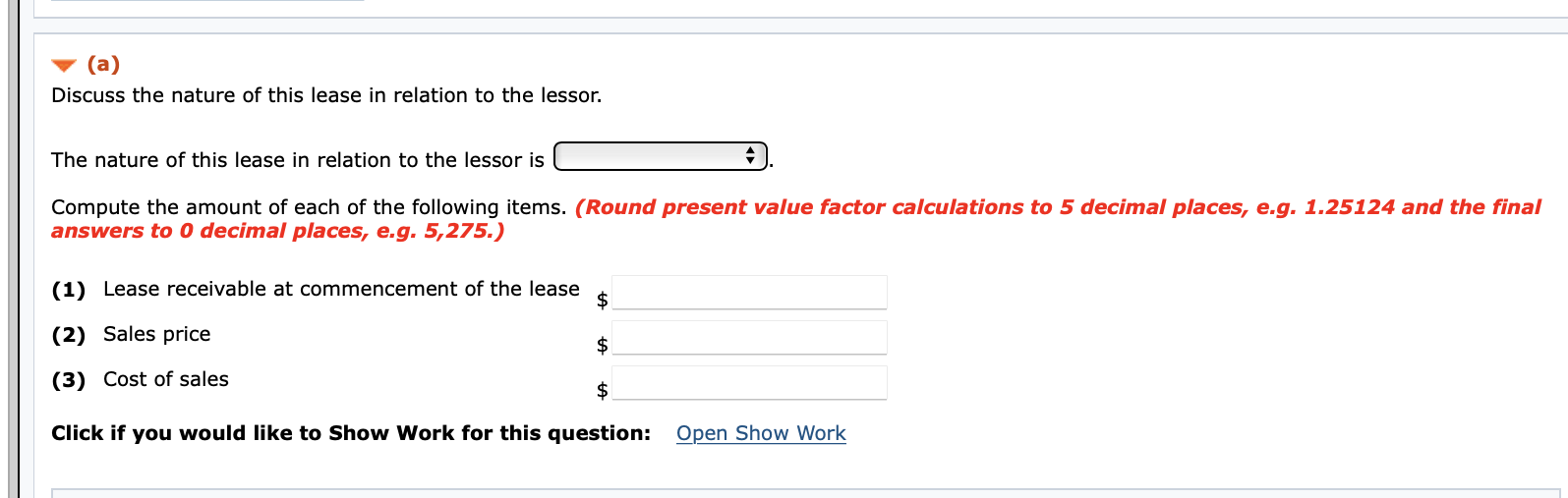
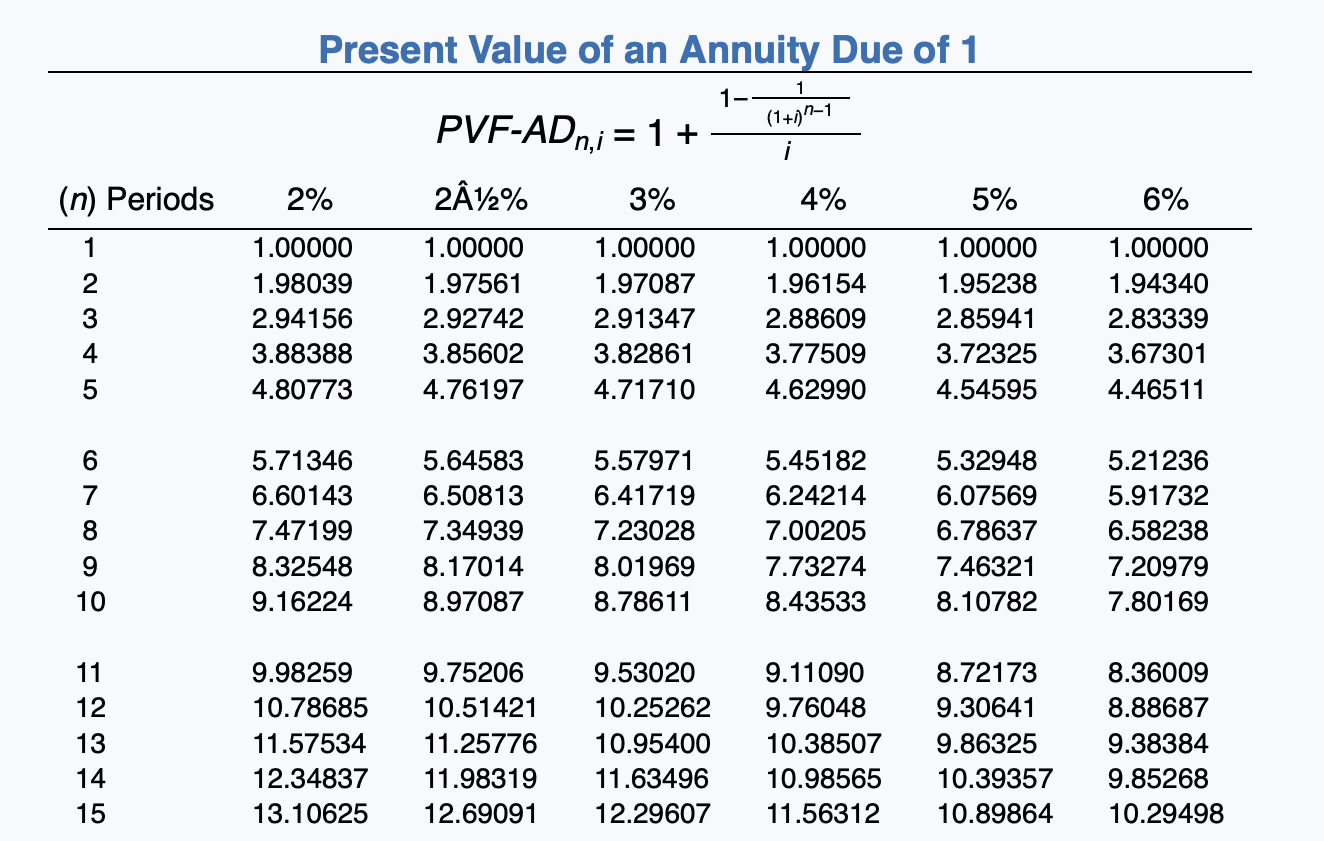
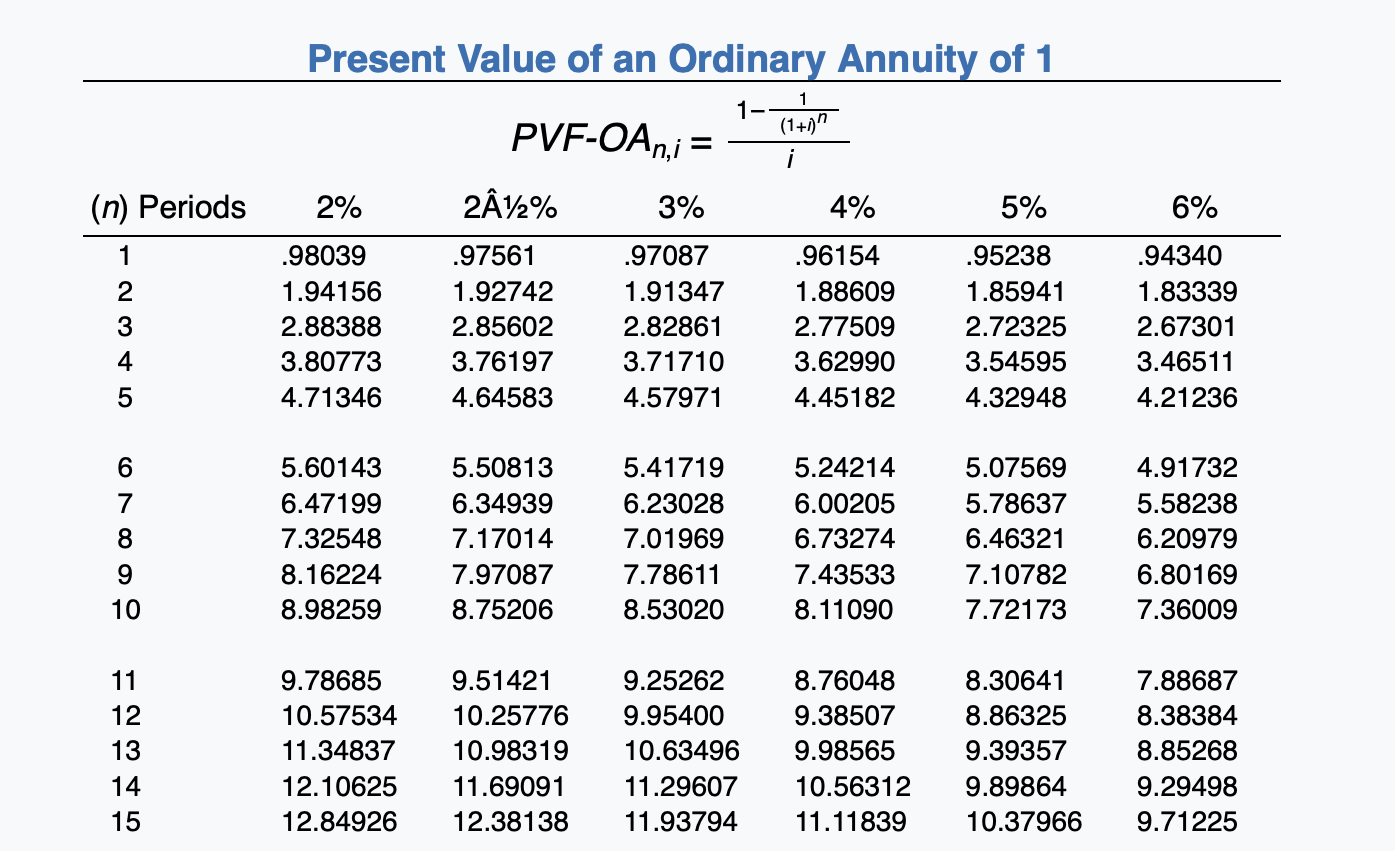
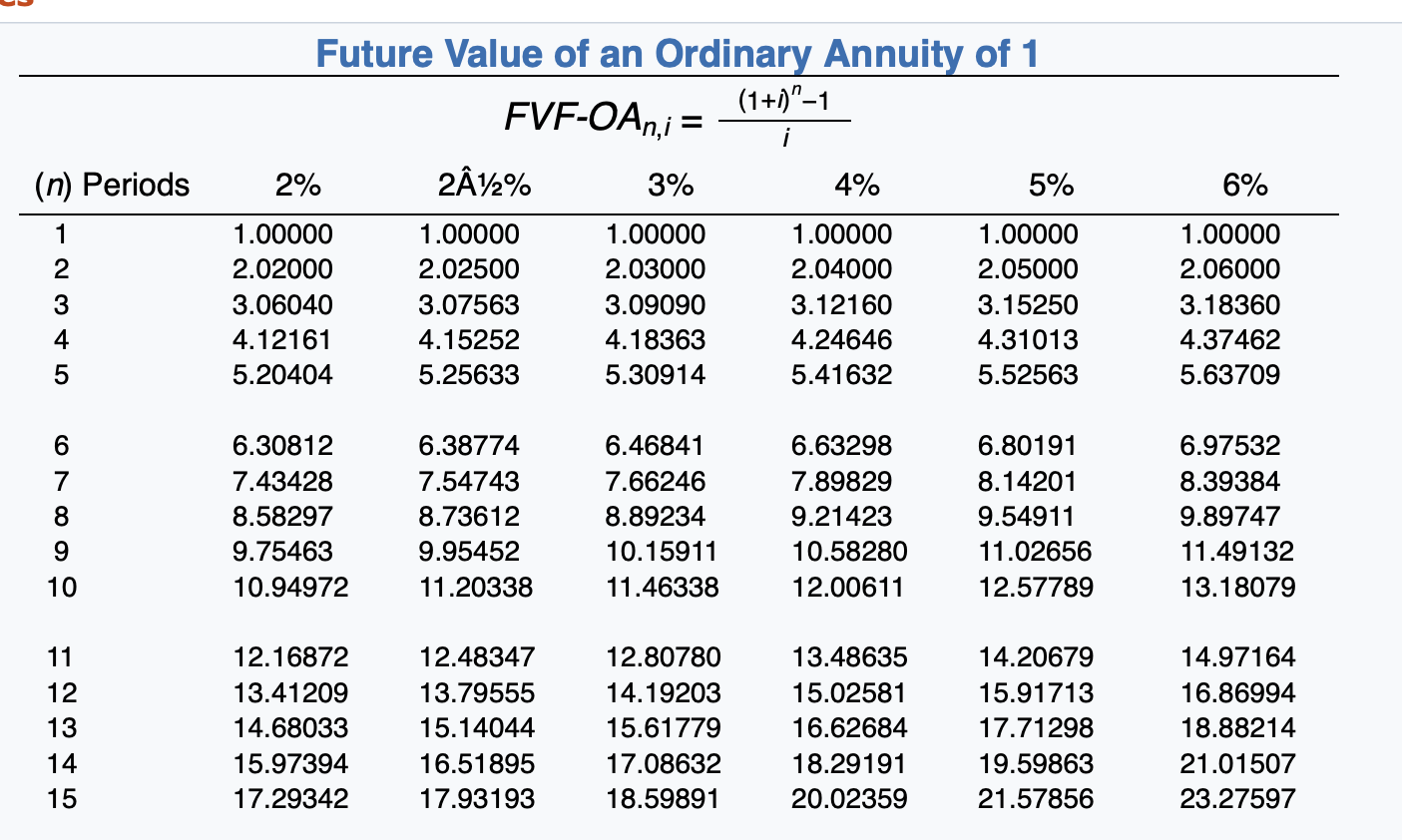
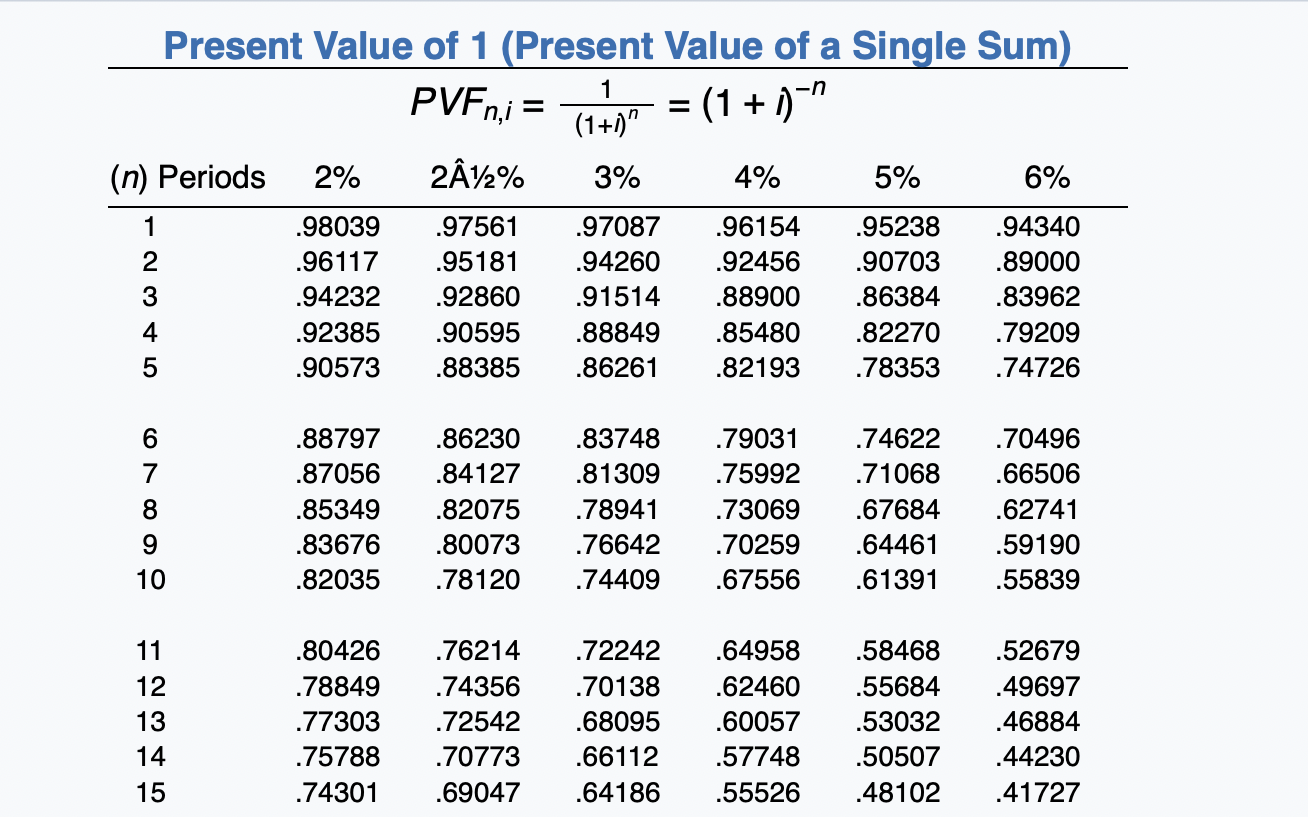
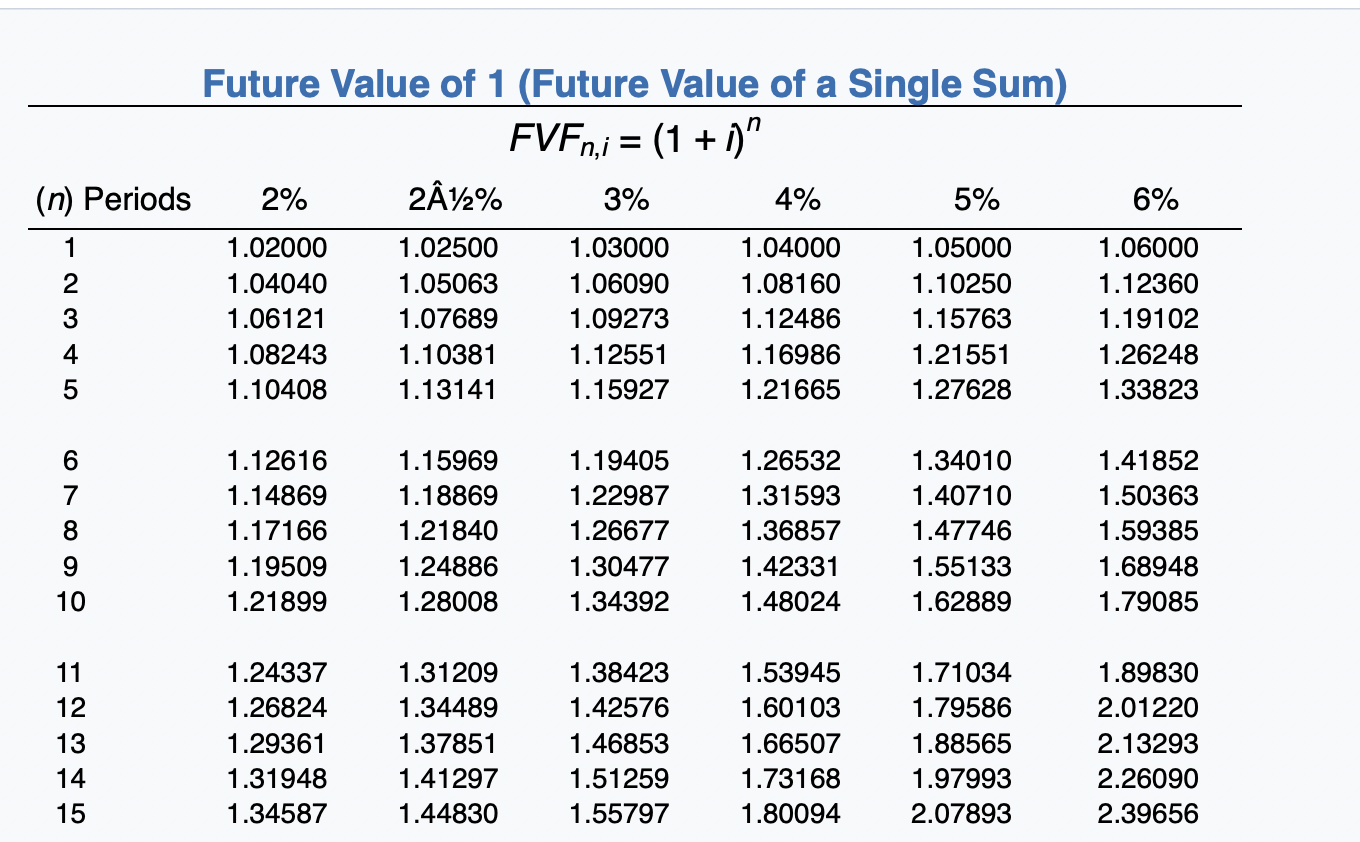
(a) Discuss the nature of this lease in relation to the lessor. The nature of this lease in relation to the lessor is Compute the amount of each of the following items. (Round present value factor calculations to 5 decimal places, e.g. 1.25124 and the final answers to 0 decimal places, e.g. 5,275.) (1) Lease receivable at commencement of the lease $ (2) Sales price $ (3) Cost of sales $ Click if you would like to Show Work for this question: Open Show Work Present Value of an Annuity Due of 1 1 1- (1+1)-1 i PVF-ADn.j = 1 + 212% 3% (n) Periods 2% 4% 5% 6% 1 2 3 4 5 1.00000 1.98039 2.94156 3.88388 4.80773 1.00000 1.97561 2.92742 3.85602 4.76197 1.00000 1.97087 2.91347 3.82861 4.71710 1.00000 1.96154 2.88609 3.77509 4.62990 1.00000 1.95238 2.85941 3.72325 4.54595 1.00000 1.94340 2.83339 3.67301 4.46511 6 7 8 5.71346 6.60143 7.47199 8.32548 9.16224 5.64583 6.50813 7.34939 8.17014 8.97087 5.57971 6.41719 7.23028 8.01969 8.78611 5.45182 6.24214 7.00205 7.73274 8.43533 5.32948 6.07569 6.78637 7.46321 8.10782 5.21236 5.91732 6.58238 7.20979 7.80169 9 10 11 12 13 14 15 9.98259 10.78685 11.57534 12.34837 13.10625 9.75206 10.51421 11.25776 11.98319 12.69091 9.53020 10.25262 10.95400 11.63496 12.29607 9.11090 9.76048 10.38507 10.98565 11.56312 8.72173 9.30641 9.86325 10.39357 10.89864 8.36009 8.88687 9.38384 9.85268 10.29498 Present Value of an Ordinary Annuity of 1 1- (1+1) PVF-OAni = i (n) Periods 2% 212% 3% 4% 5% 6% 1 2 3 4 .98039 1.94156 2.88388 3.80773 4.71346 .97561 1.92742 2.85602 3.76197 4.64583 .97087 1.91347 2.82861 3.71710 4.57971 .96154 1.88609 2.77509 3.62990 4.45182 .95238 1.85941 2.72325 3.54595 4.32948 .94340 1.83339 2.67301 3.46511 4.21236 5 6 7 8 5.60143 6.47199 7.32548 8.16224 8.98259 5.50813 6.34939 7.17014 7.97087 8.75206 5.41719 6.23028 7.01969 7.78611 8.53020 5.24214 6.00205 6.73274 7.43533 8.11090 5.07569 5.78637 6.46321 7.10782 7.72173 4.91732 5.58238 6.20979 6.80169 7.36009 9 10 12 13 14 15 9.78685 10.57534 11.34837 12.10625 12.84926 9.51421 10.25776 10.98319 11.69091 12.38138 9.25262 9.95400 10.63496 11.29607 11.93794 8.76048 9.38507 9.98565 10.56312 11.11839 8.30641 8.86325 9.39357 9.89864 10.37966 7.88687 8.38384 8.85268 9.29498 9.71225 (n) Periods 6% Future Value of an Ordinary Annuity of 1 FVF-OA= (1+1)"-1 2% 212% 3% 4% 5% 1.00000 1.00000 1.00000 1.00000 1.00000 2.02000 2.02500 2.03000 2.04000 2.05000 3.06040 3.07563 3.09090 3.12160 3.15250 4.12161 4.15252 4.18363 4.24646 4.31013 5.20404 5.25633 5.30914 5.41632 5.52563 1 2 3 1.00000 2.06000 3.18360 4.37462 5.63709 5 6 7 8 9 6.30812 7.43428 8.58297 9.75463 10.94972 6.38774 7.54743 8.73612 9.95452 11.20338 6.46841 7.66246 8.89234 10.15911 11.46338 6.63298 7.89829 9.21423 10.58280 12.00611 6.80191 8.14201 9.54911 11.02656 12.57789 6.97532 8.39384 9.89747 11.49132 13.18079 10 11 12 13 14 15 12.16872 13.41209 14.68033 15.97394 17.29342 12.48347 13.79555 15.14044 16.51895 17.93193 12.80780 14.19203 15.61779 17.08632 18.59891 13.48635 15.02581 16.62684 18.29191 20.02359 14.20679 15.91713 17.71298 19.59863 21.57856 14.97164 16.86994 18.88214 21.01507 23.27597 Present Value of 1 (Present Value of a Single Sum) PVFni = = (1 + 1) (1+1)" (n) Periods 2% 212% 3% 4% 5% 6% 1 .98039 .97561 .97087 .96154 .95238 .94340 2 .96117 .95181 .94260 .92456 .90703 89000 3 .94232 .92860 .91514 .88900 .86384 .83962 4 .92385 .90595 .88849 .85480 .82270 .79209 5 .90573 .88385 .86261 .82193 .78353 .74726 6 7 8 9 10 .88797 .87056 .85349 .83676 .82035 .86230 .84127 .82075 .80073 .78120 .83748 .81309 .78941 .76642 .74409 .79031 .75992 .73069 .70259 .67556 .74622 .71068 .67684 .64461 .61391 .70496 .66506 .62741 .59190 .55839 12 13 14 15 .80426 .78849 .77303 .75788 .74301 .76214 .74356 .72542 .70773 .69047 .72242 .70138 .68095 .66112 .64186 .64958 .62460 .60057 .57748 .55526 58468 .55684 .53032 .50507 .48102 .52679 .49697 .46884 44230 41727 6% Future Value of 1 (Future Value of a Single Sum) FVFn,i = (1 + i)" (n) Periods 2% 212% 3% 4% 5% 1 1.02000 1.02500 1.03000 1.04000 1.05000 1.04040 1.05063 1.06090 1.08160 1.10250 3 1.06121 1.07689 1.09273 1.12486 1.15763 4 1.08243 1.10381 1.12551 1.16986 1.21551 5 1.10408 1.13141 1.15927 1.21665 1.27628 1.06000 1.12360 1.19102 1.26248 1.33823 6 7 8 1.12616 1.14869 1.17166 1.19509 1.21899 1.15969 1.18869 1.21840 1.24886 1.28008 1.19405 1.22987 1.26677 1.30477 1.34392 1.26532 1.31593 1.36857 1.42331 1.48024 1.34010 1.40710 1.47746 1.55133 1.62889 1.41852 1.50363 1.59385 1.68948 1.79085 9 10 11 12 13 14 15 1.24337 1.26824 1.29361 1.31948 1.34587 1.31209 1.34489 1.37851 1.41297 1.44830 1.38423 1.42576 1.46853 1.51259 1.55797 1.53945 1.60103 1.66507 1.73168 1.80094 1.71034 1.79586 1.88565 1.97993 2.07893 1.89830 2.01220 2.13293 2.26090 2.39656












