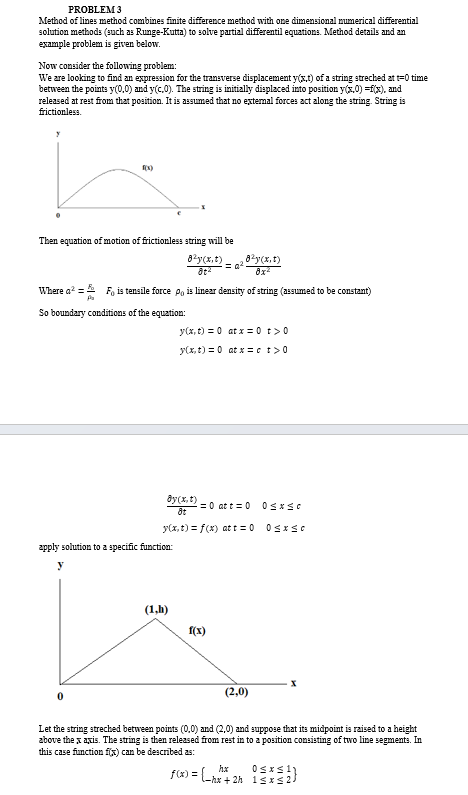
PROBLEM 3 Method of lines method combines finite difference method with one dimensional numerical differential solution methods (such as Runge-Kutta) to solve partial differentil equations. Method details and an example problem is given below. Now consider the following problem: We are looking to find an expression for the transverse displacement y(xt) of a string streched at t=0 time between the points y(0,0) and y(c.0). The string is initially displaced into position y(x,0) =f(x), and released at rest from that position. It is assumed that no external forces act along the string. String is frictionless. f(x) Then equation of motion of frictionless string will be 82y(x,t) 8t 8y(x, t) 8x Where a = F, is tensile force po is linear density of string (assumed to be constant) So boundary conditions of the equation: 8y(x, t) 8t 0 xc y(x, t) = f(x) at t=0 0xsc apply solution to a specific function: y y(x, t) = 0 atx=0 t> 0 y(x, t) = 0 at x = ct > 0 (1,h) = 0 at t=0 f(x) f(x) = (2,0) Let the string streched between points (0.0) and (2,0) and suppose that its midpoint is raised to a height above the x axis. The string is then released from rest in to a position consisting of two line segments. In this case function f(x) can be described as: 02052/ Lax + 2h