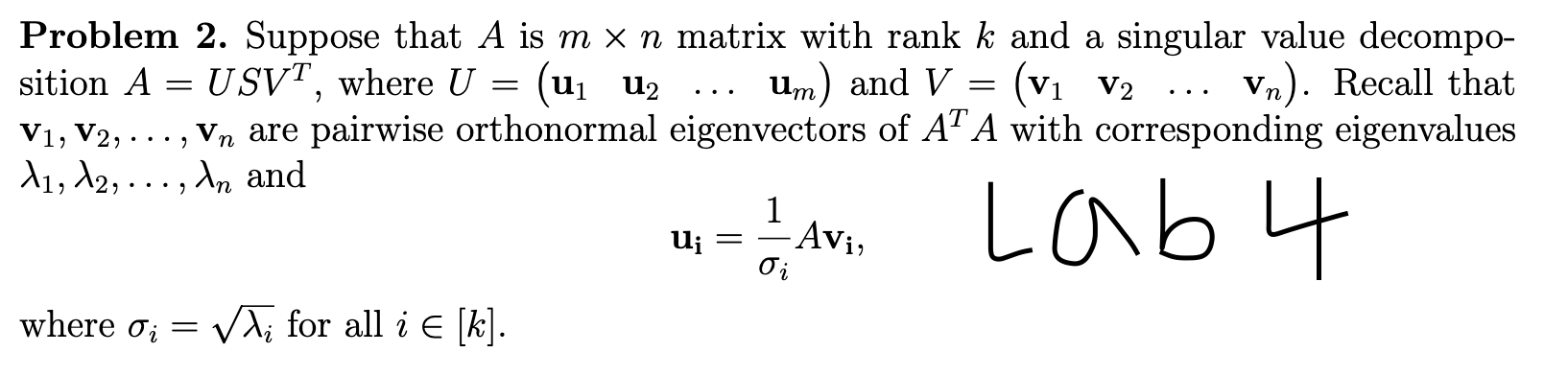
= = = Problem 3. Suppose that A is mxn matrix with rank k, singular value decomposition A USVT, and reduced singular value decomposition A = SVT, where U ( (ui u2 and V = (v1 V2 vn). Suppose that the eigenvalues of AT A satisfy l > 12 > ... > Ini (a) For all i E [n] (not just [k]), compute || Avi ||. What happens if i > k? (b) Let y E RM such that there is a w E R such that y Aw (i.e. y E Col(A)). Show there is a ze Rk such that y z (that is, show y e Col()) (Hint: w = Ci Vi + C2V2 + + Cn Vn for some constants C1, C2, ..., Cn). (c) It follows from Lab 4 (Problem 2) and (b) above that Col(A) = Col(). Show that b = projcol(a) (b) (Hint: Use the column-row expansion of T). (d) Use (c) above to verify your answer from Problem 2 (c). = = Problem 2. Suppose that A is mxn matrix with rank k and a singular value decompo- sition A U SVT, where U ui U2 um) and V (V1 V2 Vn). Recall that V1, V2, ...,Vn are pairwise orthonormal eigenvectors of AT A with corresponding eigenvalues 11, 12, ..., in and 1 Avi, Lab 4 U; = 4 O i where oi = vi for all i e [k]. = = = Problem 3. Suppose that A is mxn matrix with rank k, singular value decomposition A USVT, and reduced singular value decomposition A = SVT, where U ( (ui u2 and V = (v1 V2 vn). Suppose that the eigenvalues of AT A satisfy l > 12 > ... > Ini (a) For all i E [n] (not just [k]), compute || Avi ||. What happens if i > k? (b) Let y E RM such that there is a w E R such that y Aw (i.e. y E Col(A)). Show there is a ze Rk such that y z (that is, show y e Col()) (Hint: w = Ci Vi + C2V2 + + Cn Vn for some constants C1, C2, ..., Cn). (c) It follows from Lab 4 (Problem 2) and (b) above that Col(A) = Col(). Show that b = projcol(a) (b) (Hint: Use the column-row expansion of T). (d) Use (c) above to verify your answer from Problem 2 (c). = = Problem 2. Suppose that A is mxn matrix with rank k and a singular value decompo- sition A U SVT, where U ui U2 um) and V (V1 V2 Vn). Recall that V1, V2, ...,Vn are pairwise orthonormal eigenvectors of AT A with corresponding eigenvalues 11, 12, ..., in and 1 Avi, Lab 4 U; = 4 O i where oi = vi for all i e [k]