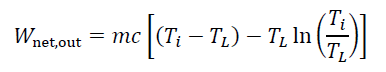
Problem 5 (20 points) - Numerical Approach to Problem 4 Consider the same physical situation as in Problem 4: a Carnot engine powered by an incompressible, finite thermal energy source with constant specific heat thermalizing with the surrounding infinite thermal sink. Let's develop numerical approximations to the exact solution developed in Problem 4. Our numerical approximations will be based on finite amounts of energy transfer. As the finite amounts of energy transfer get smaller, our numerical solution should approach the analytical solution to within acceptable error. We must first develop our understanding of the numerical problem. If we consider K finite heat transfers into the engine during the equilibrating process resulting in K finite amounts of net work produced by the engine, the total net work produced is Wnet,out k=1 Wk= QH,k nk k=1 where the subscript k indicates that QH and n might change for every W. We must now think about how to define QH,k and nk. Since the temperature of the thermal energy source is the fundamental property that is changing throughout the equilibration process, we want to cast all important quantities in terms of this temperature. It seems reasonable to consider the temperature changing in a series of equally sized intervals. So, for K intervals, the relationship between the source temperature at the beginning of the kth and (k + 1)th intervals is Tx+1 = Tk - Ti-TL. Now let's piece together the rest of the numerical puzzle. K a) During the kth interval, the energy source temperature changes from T to Tx+1. Develop an expression for the kth amount of heat transfer into the Carnot engine in terms of Tx, Tx+1, m, and c. b) Now consider the efficiency of the Carnot engine during the kth interval. Should we take the temperature of the thermal source to be the temperature at the beginning of the kth interval (Tx), the end (Tx+1)? Come up with a reasonable temperature to use for the temperature of the thermal source during the kth interval. Write down your expression for Mk. c) Combine your results to develop an expression for the net work output of the Carnot engine during the kth interval (WR). d) Now use your above results to write a computer program that can calculate the net work output of the Carnot engine using the numerical expressions developed in parts (a)-(c). Set your program up so that it will start by using a single finite interval and increase the number of intervals until the error between the numerical result for Wnet,out is within 0.1% of the exact result determined in Problem 4. For concreteness, use m = 100 kg, c = 5 kJ/kg-K, T = 300 K, and T = 500 K. e) Plot the exact solution, the numerical solution, and the error between the exact solution and the numerical solution as a function of the number of intervals on the same figure. Wnet,out - = mc | (T T) T In ( -