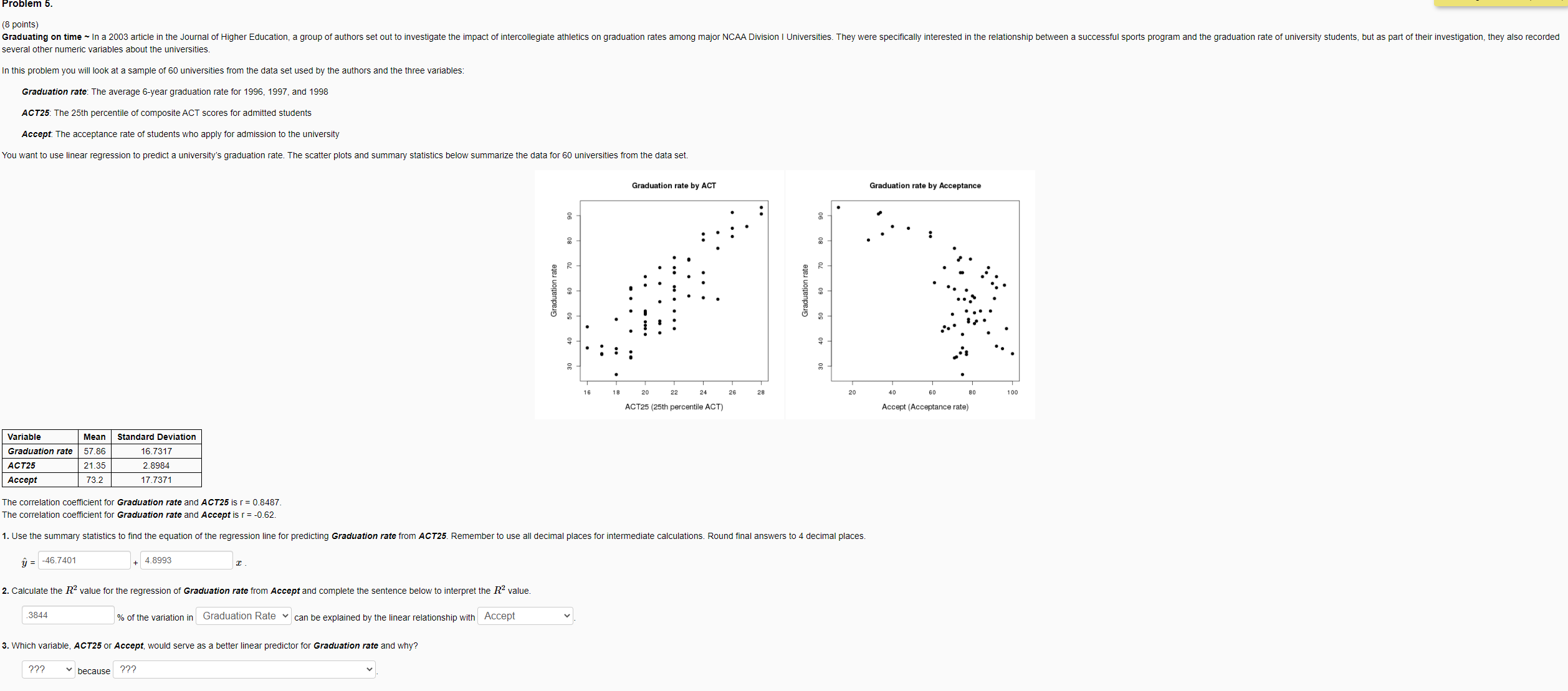
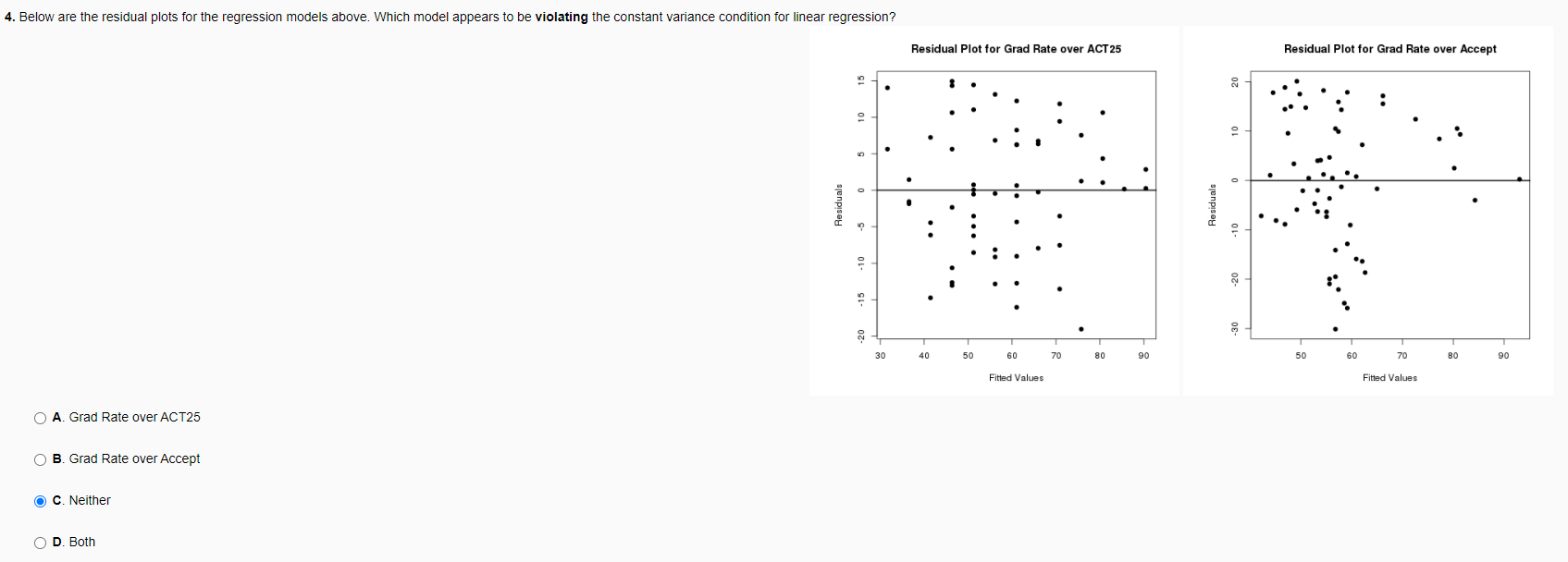
Problem 5. (8 points) Graduating on time ~ In a 2003 article in the Journal of Higher Education, a group of authors set out to investigate the impact of intercollegiate athletics on graduation rates among major NCAA Division I Universities. They were specifically interested in the relationship between a successful sports program and the graduation rate of university students, but as part of their investigation, they also recorded several other numeric variables about the universities. In this problem you will look at a sample of 60 universities from the data set used by the authors and the three variables: Graduation rate: The average 6-year graduation rate for 1996, 1997, and 1998 ACT25. The 25th percentile of composite ACT scores for admitted students Accept: The acceptance rate of students who apply for admission to the university You want to use linear regression to predict a university's graduation rate. The scatter plots and summary statistics below summarize the data for 60 universities from the data set. Graduation rate by ACT Graduation rate by Acceptance 90 90 80 80 70 R Graduation rate Graduation rate 60 50 40 16 18 20 22 24 26 28 20 40 80 100 ACT25 (25th percentile ACT) Accept (Acceptance rate) Variable Mean Standard Deviation Graduation rate |57.86 16.7317 ACT2 21.35 2.8984 Accept 73.2 17.7371 The correlation coefficient for Graduation rate and ACT25 is r = 0.8487. The correlation coefficient for Graduation rate and Accept is r = -0.62. 1. Use the summary statistics to find the equation of the regression line for predicting Graduation rate from ACT25. Remember to use all decimal places for intermediate calculations. Round final answers to 4 decimal places y = -46.7401 + 4.8993 2. Calculate the R2 value for the regression of Graduation rate from Accept and complete the sentence below to interpret the R value. 3844 % of the variation in Graduation Rate |can be explained by the linear relationship with Accept 3. Which variable, ACT25 or Accept, would serve as a better linear predictor for Graduation rate and why? ??? because ???4. Below are the residual plots for the regression models above. Which model appears to be violating the constant variance condition for linear regression? Residual Plot for Grad Rate over ACT 25 Residual Plot for Grad Rate over Accept C Residual Residual -10 -10 -20 -30 50 60 70 80 90 30 40 50 60 70 80 90 Fitted Values Fitted Values O A. Grad Rate over ACT25 O B. Grad Rate over Accept O C. Neither O D. Both