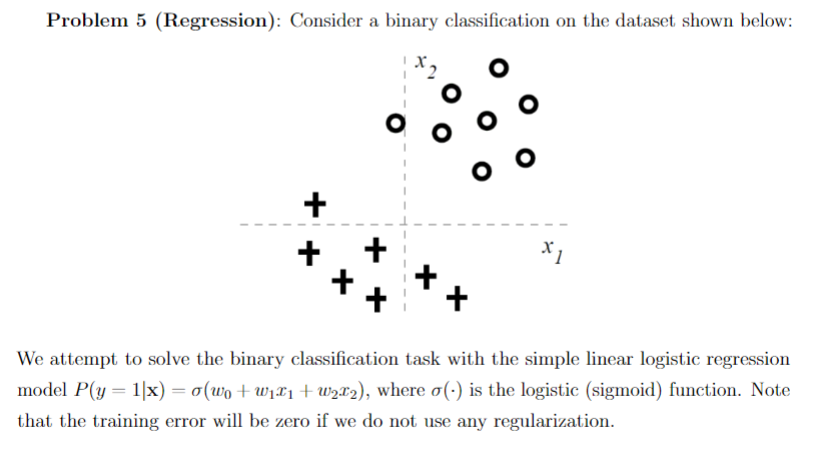

Problem 5 (Regression): Consider a binary classification on the dataset shown below: + + x] We attempt to solve the binary classification task with the simple linear logistic regression model P(y=1) = (wo + w121 + W212), where o() is the logistic (sigmoid) function. Note that the training error will be zero if we do not use any regularization. Now let us consider training a regularized linear logistic regression models where we try to minimize: J(w) = -l(w, Dtrain) + Cw; where l(w, Dtrain) is the log-likelihood on the training data. The regularization used in J(w) is Cw, where j = {0,1,2}. In other words, only one of the parameters is regularized in each case. (a) Given the training data shown in the figure, suppose we regularize w and set C to be very large. Does the training error increase or stay the same (zero) for very large C? Briefly explain. (b) Following previous question, what if we regularize w instead and set C to be very large? Briefly explain. (C) What if we regularize wo instead and set C to be very large? Briefly explain. (d) If we instead set C to be a very small number (close to 0). What the decision boundary will look like when regularing w2? Draw a possible decision boundary in the figure. (Ilint: 1. The decision boundary (wo + w121 + w212 = 0) of logistic regression is linear; 2. When you set C to be very large, it pushs the regularizing term to be zero. Then think of what it means for the linear decision boundary.) Problem 5 (Regression): Consider a binary classification on the dataset shown below: + + x] We attempt to solve the binary classification task with the simple linear logistic regression model P(y=1) = (wo + w121 + W212), where o() is the logistic (sigmoid) function. Note that the training error will be zero if we do not use any regularization. Now let us consider training a regularized linear logistic regression models where we try to minimize: J(w) = -l(w, Dtrain) + Cw; where l(w, Dtrain) is the log-likelihood on the training data. The regularization used in J(w) is Cw, where j = {0,1,2}. In other words, only one of the parameters is regularized in each case. (a) Given the training data shown in the figure, suppose we regularize w and set C to be very large. Does the training error increase or stay the same (zero) for very large C? Briefly explain. (b) Following previous question, what if we regularize w instead and set C to be very large? Briefly explain. (C) What if we regularize wo instead and set C to be very large? Briefly explain. (d) If we instead set C to be a very small number (close to 0). What the decision boundary will look like when regularing w2? Draw a possible decision boundary in the figure. (Ilint: 1. The decision boundary (wo + w121 + w212 = 0) of logistic regression is linear; 2. When you set C to be very large, it pushs the regularizing term to be zero. Then think of what it means for the linear decision boundary.)








