Problem 5. The max-bottleneck path problem: Given a weighted undirected graph G = (V,E) with non-negative weights w(u,v) for each edge {u,v} 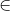E, suppose the weight w(u,v) represents the max-capacity of a message sent along the edge {u,v}. (Alternatively, you can consider the edges as roads and the weights as the heights of the bridges above these roads.) Thus, the bottleneck along a path () is 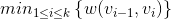. A max-bottleneck path between u and v is a path whose bottleneck is the largest among all paths connecting u and v. Given a starting vertex s, propose an algorithm in pseudocode to find the max-bottleneck path from s to every other node in V . **Prove the correctness of your algorithm and analyze its running time**.