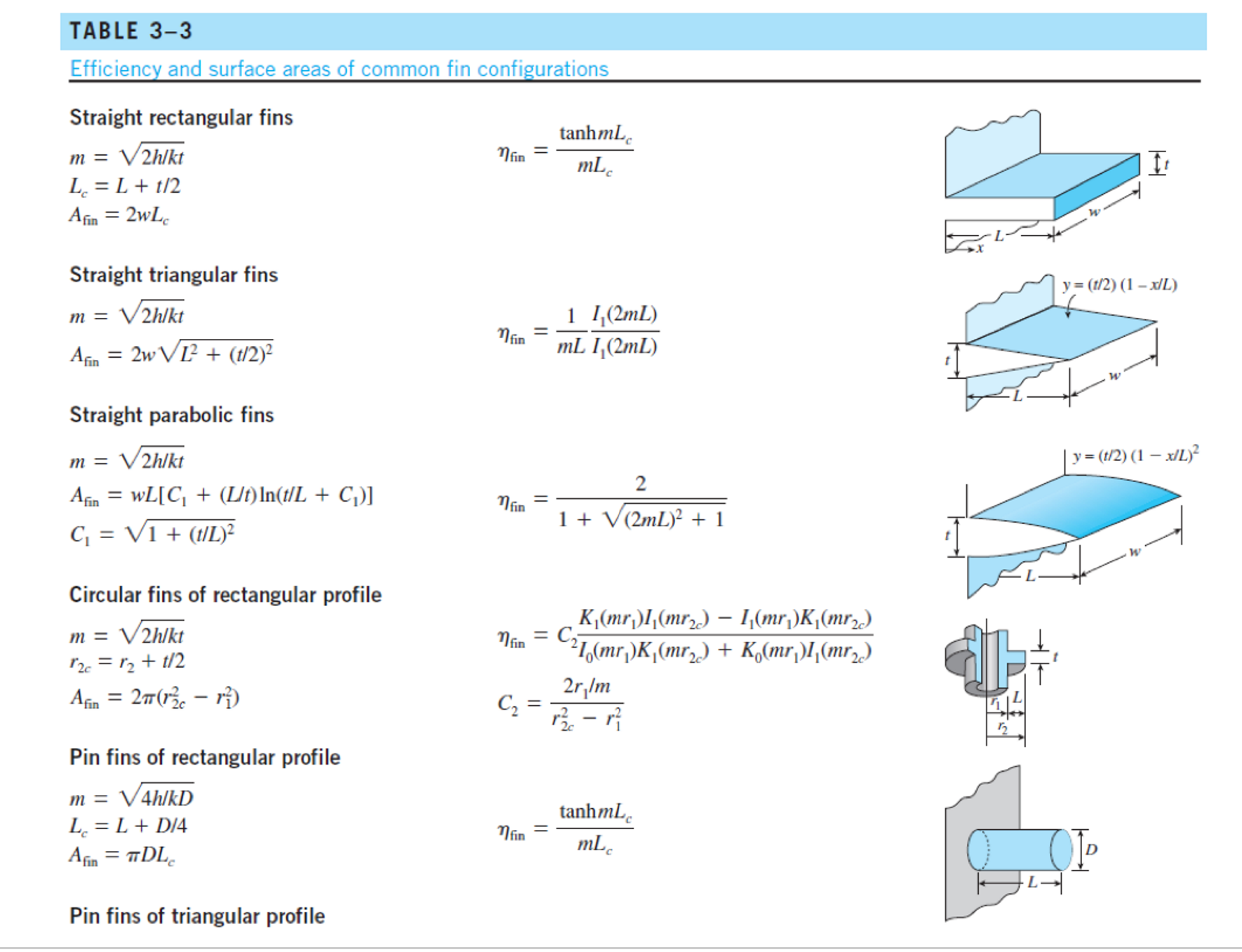
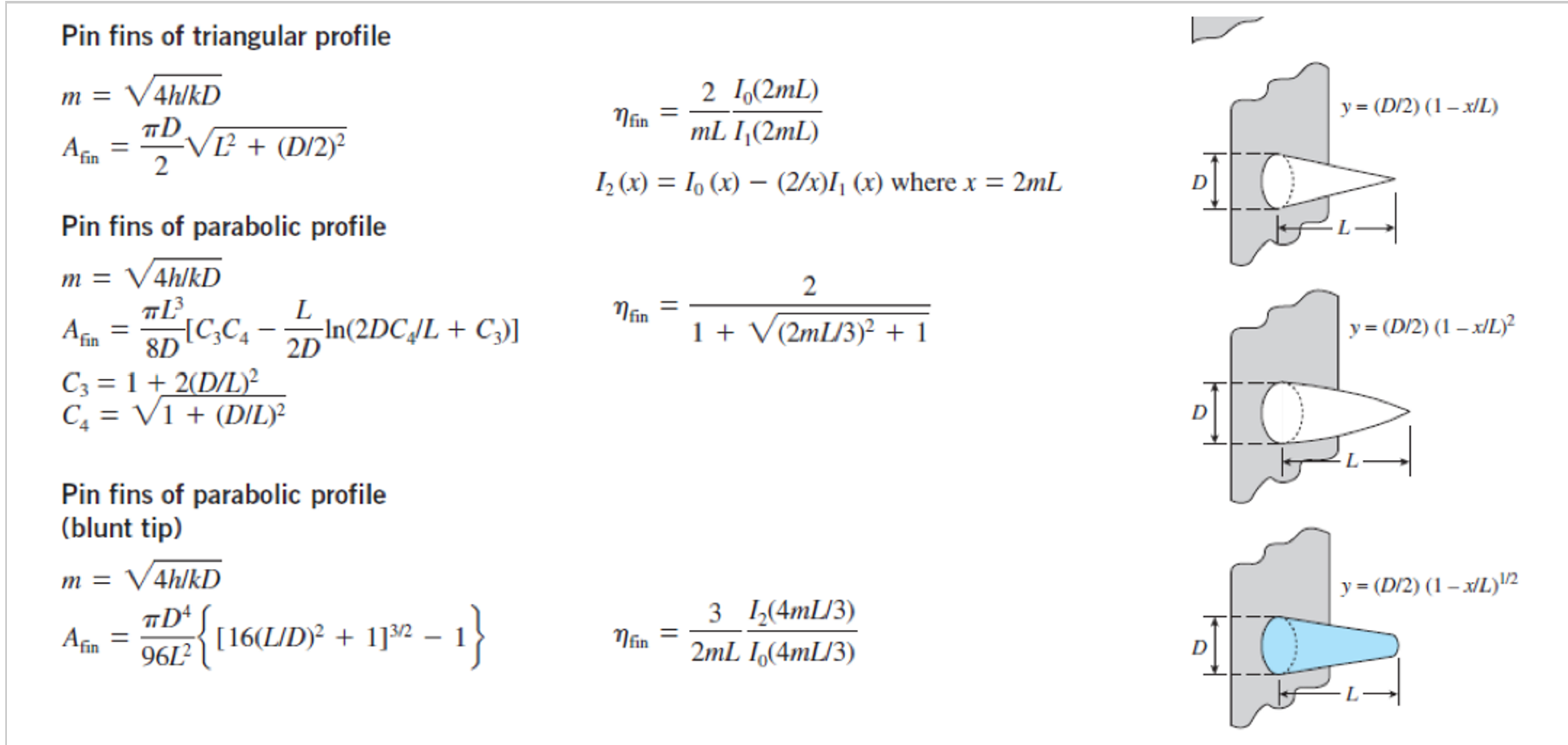
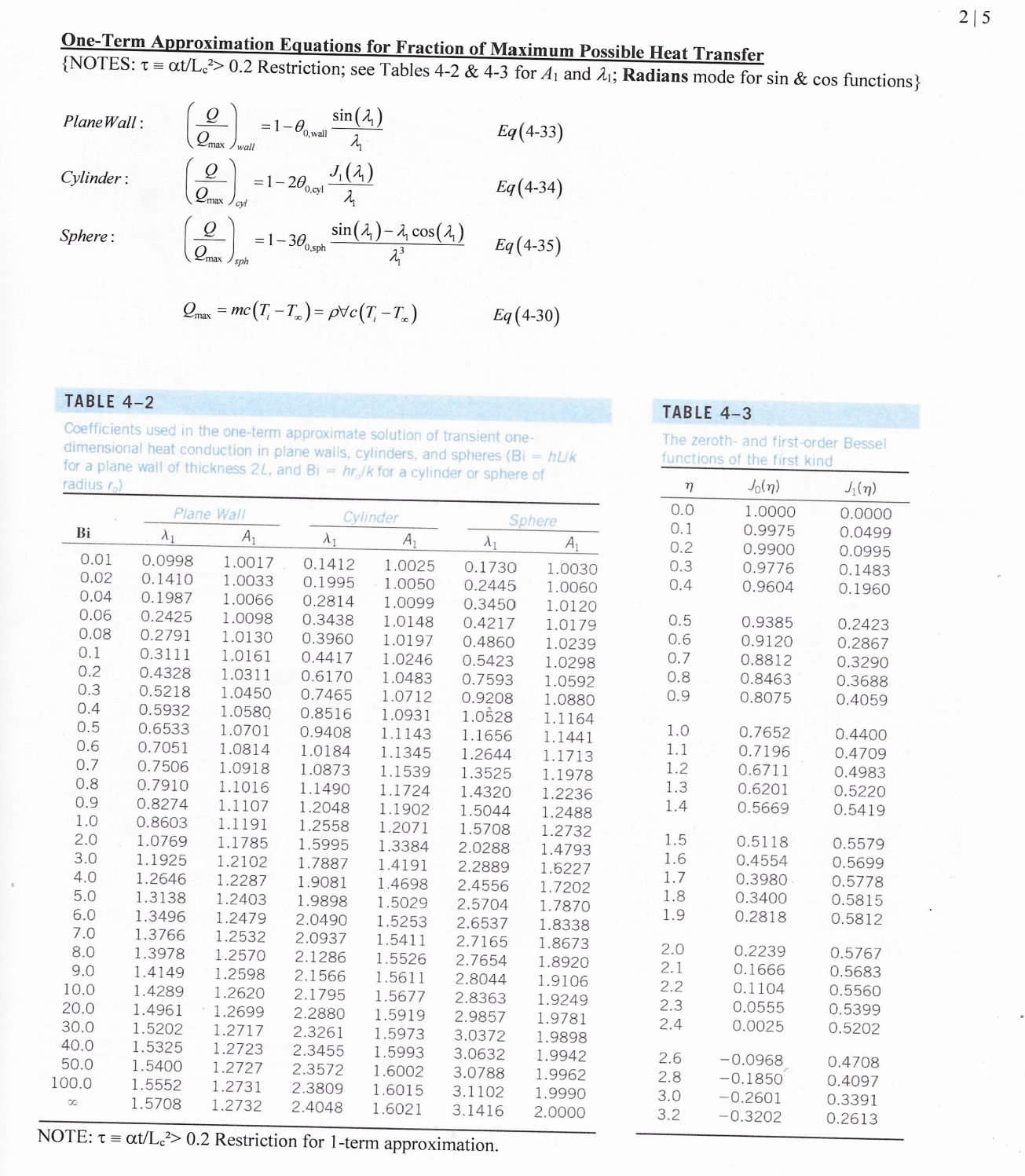
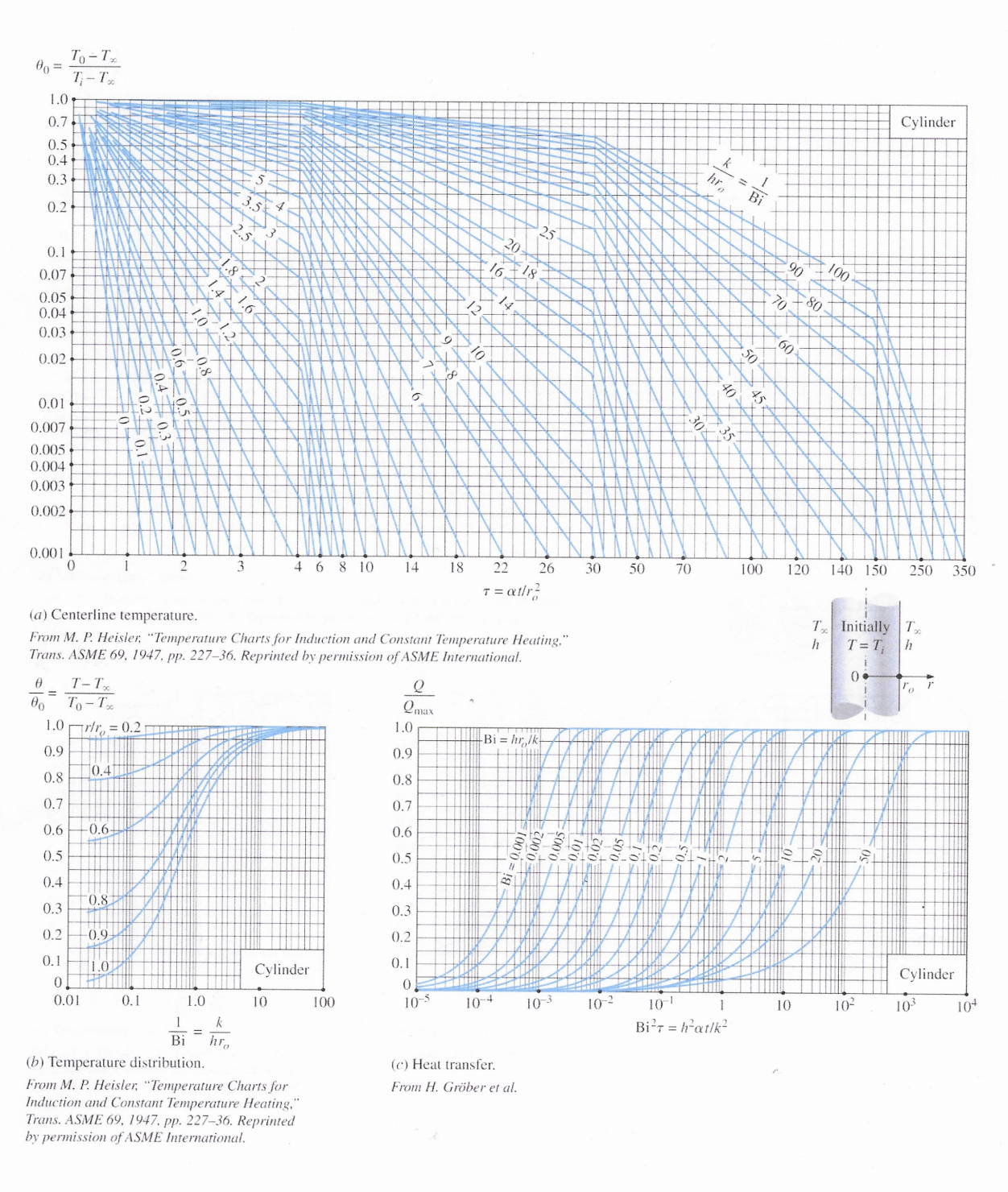
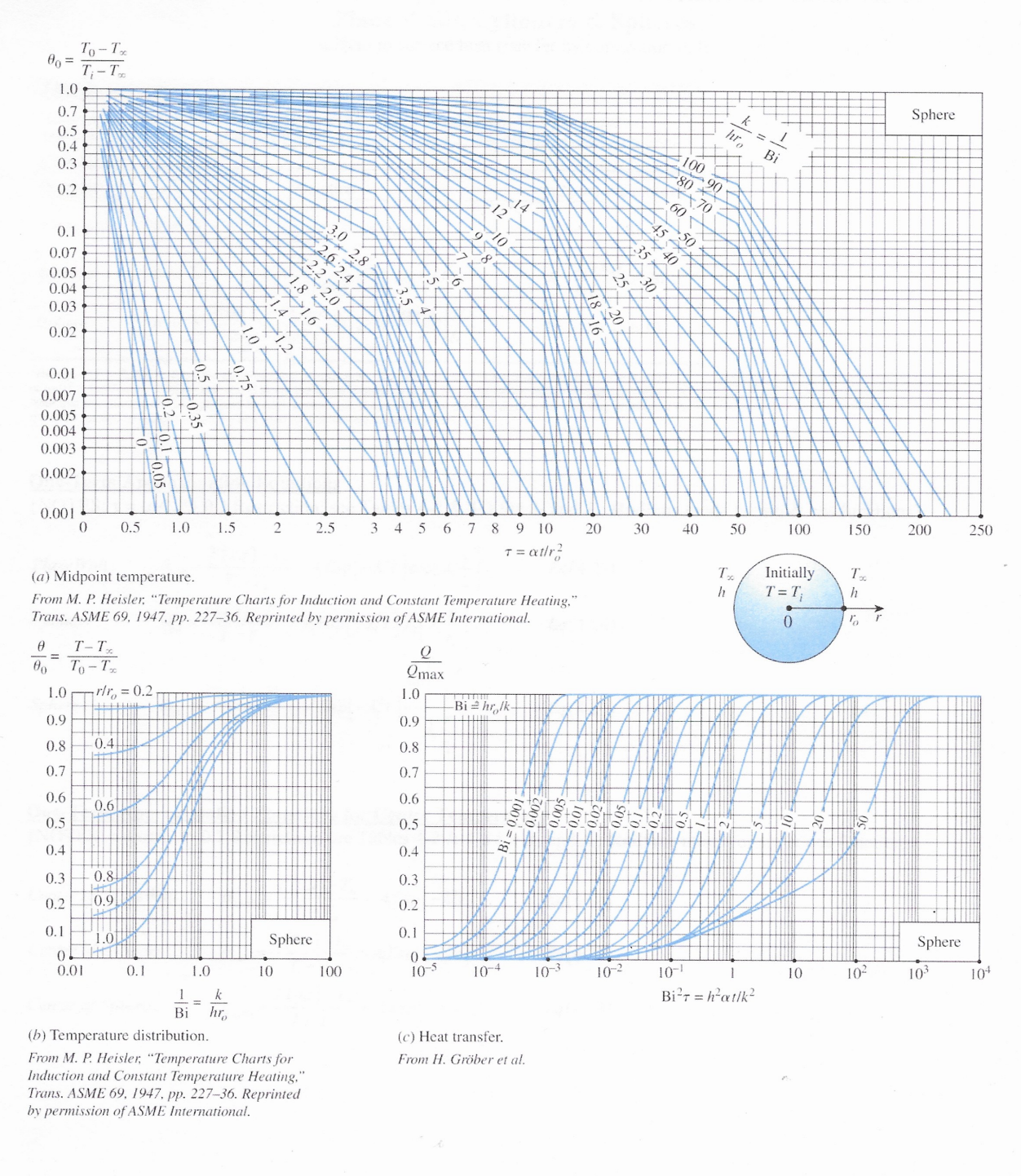
Problem 9 (50 Points) An air-cooled aluminum heat sink is used to keep electronics cool (see image and diagram). The cooling requirements are being significantly increased. To increase the rate of cooling, two options are being considered: 1) increase the velocity of the air by 40% (to increase the convective heat transfer coefficient); and 2) increase the length (L) of the fin by 40% (to increase the surface area, but h decreases by 18%). The fin's base temperature is 70C. The air temperature 15C. At an air velocity of 5 m/s, h=55.97 W/m-C. The thermal conductivity of aluminum, k = 239.3 W/m-C. The dimensions of the rectangular fins and air-gap spacing between fins are: L = 2.5 mm; W = 34.65 mm; t = 0.1 mm; b = 2.5 mm. 1cm 2 Tease 34.65 For the Base Case (i.e., 2.5mm long rectangular fins, and 5 m/s air flow with h = 55.97 W/m-C), calculate the following {Hint: Use Table 3-3}: a) mL for the fin: {#.####} b) The fin efficiency, n = {##.##%} c) The fin area, Ac =. {###.# mm} d) The maximum rate of heat transfer for the fin: {#.#### W} e) The actual rate of heat transfer for the fin: {#.#### W} For Case 1 (i.e., 2.5mm long rectangular fins, and 7 m/s air flow with h = 64.71 W/m-C), calculate the following: f) mL for the fin: {#.####} g) The fin efficiency, n = {##.##%} h) The fin area, Ac = {###.# mm} i) The maximum rate of heat transfer for the fin: {#.#### W} 0.1 3.50 2.50 j) The actual rate of heat transfer for the fin: {#.#### W} k) The increase in the actual rate of heat transfer (i.e., (J - E)/E *100): For Case 2 (i.e., 3.5mm long rectangular fins, and 5 m/s air flow with h = 47.30 W/m-C), calculate the following: 1) mL for the fin: {##.##%} {#.####} m) The fin efficiency, n = {##.##%} n) The fin area, Ac =. {###.# mm} o) The maximum rate of heat transfer for the fin: p) The actual rate of heat transfer for the fin: {#.#### W} {#.#### W} q) The increase in the actual rate of heat transfer (i.e., (P - E)/E *100): Based on your analysis which method yields the better increase in cooling capacity? Case 1: Increase the air flow through the fin array. Case 2: Increase the length of the fins to increase heat transfer surface area (even though h went down by 18%). {##.##%} TABLE 3-3 Efficiency and surface areas of common fin configurations Straight rectangular fins m = V2h/kt L = L + 1/2 tanhmL nfin = mL Afin = 2wLc Straight triangular fins m = V2h/kt y= (1/2) (1-x/L) nfin Afin = 2w L + (t/2) 1 I(2mL) mL I(2mL) w Straight parabolic fins y = (t/2) (1 - x/L) m = V2hlkt 2 Afin = WL[C + (L/t) In(t/L + C)] nfin 1 + V (2mL) + 1 t C = 1 + (1/L) Circular fins of rectangular profile m = V2h/kt 12c = 12 + 1/2 Afin = 2 (1-1) Pin fins of rectangular profile m = 4h/kD L = L+D/4 Afin = DLC Pin fins of triangular profile K(mr)I(mr) I(mr)K(mr2) 21(mr)K(mr) + K(mr)I(mr) nfin = C 2r/m C = tanhmL = Mfin mLc 12 Pin fins of triangular profile 2 I(2mL) nfin mL I(2mL) 12(x) = 10 (x) - (2/x)I (x) where x = 2mL y = (D/2) (1-x/L) 2 1 + (2mL/3) + 1 m = 4h/kD D = 1 + (D/2) 2 Afin Pin fins of parabolic profile m = 4h/kD L Aim = TDIC,C4 - In(2DC /L + C)] An 8D C3 = 1 + 2(D/L) C = 1 + (DIL) 2D Pin fins of parabolic profile (blunt tip) m = 4h/kD Afin = D4 961 {[16(L/D) + 1]/2 nfin 2- 1} nfin = 3 12(4mL/3) 2mL 10(4mL/3) y= (D/2) (1-x/L) y = (D/2) (1-x/L)1/2 TABLE 4-1 Summary of the solutions for one-dimensional transient conduction in a plane wall of thickness 2L, a cylinder of radius r, and a sphere of radius r. subjected to convention from all surfaces.* A's are the roots of Geometry Solution 4 sin A, Plane wall 0 = e-cos (Ax/L) A,, tan A,, = Bi 2A + sin(2A) 2 J(AR) J(A) Cylinder 0 = e-Jo (Arr) = Bi A J (A) + J} (A) Jo (Am) 4(sin A - A cos ) Sphere 0 = e-== 2A, sin (A,,x/L) Ax/L 1-A,, cot A, Bi sin(2A) AL *Here @ (TT)/(TT) is the dimensionless temperature, BihL/k or hr, /k is the Biot number, Fo= T = at/L or ar/r2 is the Fourier number, and Jo and J are the Bessel functions of the first kind whose values are given in Table 4-3. Note that the characteristic length used for each geometry in the equations for the Biot and Fourier numbers is different for the exact (analytical) solution than the one used for the lumped system analysis. One-Term Approximation Equations {NOTES: = at/Lc2> 0.2 Restriction; see Tables 4-2 & 4-3 for A and 21; Radians mode for sin & cos functions} Plane Wall: 0. = T(x,t)-Tx wall T-T = A,Exp[-]cos ]00[4] Eq(4-23) Cylinder: Ocvl = T(r,t)-T T-T = 4, Exp [1}t] J [1, Eq(4-24) r sin T(r.)-T-A Exp[-] Sphere: sph T-T Eq(4-25) r ro One-Term Approximation Equations for Center Temperature {NOTES: t = at/Lc> 0.2 Restriction; see Tables 4-2 & 4-3 for 41 and 21; Radians mode for sin & cos functions} Center of Plane Wall: Center of Cylinder: Center of Sphere: T(0.1)-T = AExp[-] Eq(4-26) 00,wall T-T T(0,1)-T = A Exp[-x+] Eq(4-27) 00,cyl T-T T(0,t)-T AExp[-2] Eq(4-28) 00,sph T-T One-Term Approximation Equations for Fraction of Maximum Possible Heat Transfer {NOTES: Tat/Le2> 0.2 Restriction; see Tables 4-2 & 4-3 for A and 21; Radians mode for sin & cos functions} sin() 215 Q Plane Wall: =1-00,wall Eq(4-33) Qmax wall Q J(2) Cylinder: =1-200.cyl Eq(4-34) max cyl Q Sphere: =1-30 0,sphi Qmax sin()- cos(4) 23 Eq (4-35) sph 2max =mc(T-T)= pvc (T-T) Eq (4-30) TABLE 4-2 Coefficients used in the one-term approximate solution of transient one- dimensional heat conduction in plane walls, cylinders, and spheres (Bi = huk for a plane wall of thickness 2L, and Bi=hrolk for a cylinder or sphere of radius ro) TABLE 4-3 The zeroth- and first-order Bessel functions of the first kind n Jo(n) J(n) 0.0 1.0000 0.0000 Plane Wall Cylinder Sphere 0.1 Bi A 0.01 0.0998 1.0017 0.02 0.1410 1.0033 0.04 0.1987 1.0066 0.06 0.2425 1.0098 0.08 0.2791 1.0130 A A 0.1412 1.0025 0.1730 0.1995 1.0050 0.2445 A 0.2 1.0030 0.3 1.0060 0.4 7234 0.9975 0.0499 0.9900 0.0995 0.9776 0.1483 0.9604 0.1960 0.2814 1.0099 0.3450 1.0120 0.3438 1.0148 0.4217 0.5 1.0179 0.9385 0.2423 0.3960 1.0197 0.4860 1.0239 0.6 0.9120 0.2867 0.1 0.3111 1.0161 0.4417 1.0246 0.5423 1.0298 0.7 0.8812 0.3290 0.2 0.4328 1.0311 0.6170 1.0483 0.7593 1.0592 0.8 0.8463 0.3688 0.3 0.5218 1.0450 0.7465 1.0712 0.9208 1.0880 0.9 0.8075 0.4059 0.4 0.5932 1.0580 0.8516 1.0931 1.0528 1.1164 0.5 0.6533 1.0701 0.9408 1.0 1.1143 0.7652 0.4400 1.1656 1.1441 0.6 0.7051 1.0814 1.0184 1.1 1.1345 0.7196 1.2644 1.1713 0.4709 0.7 0.7506 1.0918 1.2 1.0873 0.6711 1.1539 1.3525 1.1978 0.4983 0.8 0.7910 1.1016 1.3 1.1490 0.6201 1.1724 0.5220 0.9 0.8274 1.1107 1.2048 1.0 0.8603 1.1191 1.2558 2.0 1.0769 1.1785 1.5995 1.4320 1.1902 1.5044 1.2488 1.2071 1.5708 1.2732 1.3384 2.0288 1.2236 1.4 0.5669 0.5419 1.5 0.5118 0.5579 1.4793 1.6 0.4554 0.5699 3.0 1.1925 1.2102 1.7887 1.4191 2.2889 1.6227 1.7 0.3980 0.5778 4.0 1.2646 1.2287 1.9081 1.4698 2.4556 1.7202 1.8 0.3400 0.5815 5.0 1.3138 1.2403 1.9898 1.5029 2.5704 1.7870 1.9 0.2818 0.5812 6.0 1.3496 1.2479 2.0490 1.5253 2.6537 1.8338 7.0 1.3766 1.2532 2.0937 1.5411 2.7165 1.8673 2.0 0.2239 0.5767 8.0 1.3978 1.2570 2.1286 1.5526 2.7654 1.8920 2.1 0.1666 0.5683 9.0 1.4149 1.2598 2.1566 1.5611 2.8044 1.9106 2.2 0.1104 0.5560 10.0 1.4289 1.2620 2.1795 1.5677 2.8363 1.9249 2.3 0.0555 0.5399 20.0 1.4961 1.2699 2.2880 30.0 1.5202 1.2717 2.3261 40.0 50.0 100.0 00 1.5919 1.5973 3.0372 1.9898 1.5325 1.2723 2.3455 1.5993 3.0632 1.9942 1.5400 1.2727 2.3572 1.6002 3.0788 1.9962 1.5552 1.2731 2.3809 1.6015 3.1102 1.5708 1.2732 2.4048 1.6021 3.1416 2.9857 1.9781 2.4 0.0025 0.5202 2.6 -0.0968 0.4708 2.8 -0.1850 0.4097 1.9990 3.0 -0.2601 0.3391 2.0000 3.2 -0.3202 0.2613 NOTE: Tat/L> 0.2 Restriction for 1-term approximation. To-Tx 00 = T-T 1.0 0.7 0.5+ 0.4+ 0.3 0.2 0.1 0.07 0.05 0.04 0.03 1.0 0.7 0.5 0.8 0.6: 6 14 k 1 hL Bi 10 9 8 25 100 90 80 ++70 60 45-50 35 40' Plate 0.02 20.4 S 8 0.01 18.30 0.007 0.005 0.004 0.003 0.002 1 0.001 0 1 2 3 46810 14 18 22 26 30 50 70 100 120 150 300 400 500 600 700 T = t/L (a) Midplane temperature. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. Tx Initially T h T = Ti h 0 L 1 2L # == 80 T-T To-Tx 1.0 x/L = 0.2 Qmax 1.0 0.9 0.9 Bi=hL/k 0.4 0.8 0.8 0.7 0.7 0.6 0.6 0.6 0.5 0.5 0.002: 0.4 0.8 0.4 0.3 0.3 0.9 0.2 0.2 0.1 1.0 0.1 Plate 0 Plate 0 0.01 0.1 1.0 10 100 10-5 10-4 10-3 10-2 10-1 1 10 102 103 10+ 1 k Bir = hatlk = Bi hL (b) Temperature distribution. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. (c) Heat transfer. From H. Grber et al. To-Tx T-T% 00 = 1.0 0.7 0.5 0.4 0.3 0.2 0.1 0.07 0.05 0.04 0.03 0.02 0.01 0.007 0.005 0.004 0.003 0.002 3.5 2.5 1.8 1.42 1.0 1.6 0 e Bi hro 100 90 70-80. 50 40 60 45 25 20 18 16. 14. 12 10 30 Cylinder 0.001 0 1 2 3 46810 14 18 22 26 30 50 70 100 120 140 150 250 350 T = atir (a) Centerline temperature. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. h T Initially T T=T h 0 ro T-Tx = 80 To-T% Qmax 1.0 rlr=0.2 1.0 Bi=hrlk 0.9 0.9 10.4 0.8 0.8 0.7 0.7 0.6 -0.6- 0.6 0.5 0.5 100'0 = 0.002 .005 0.01 B 0.4 0.4 0.8 0.3 0.3 0.2 -0.9 0.2 0.1 = 0.1 1.0 Cylinder Cylinder 0 0 0.01 0.1 1.0 10 100 10-5 10-4 10-3 10-2 10-1 1 10 10 103 10+ 1 k Bir=hatlk = Bi hro (b) Temperature distribution. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. (c) Heat transfer. From H. Grber et al. 80= 1.0 To-Tx T-T 0.7 0.5 0.4 0.3 0.2 0.1 0.07 0.05 0.04 0.03 0.02 1.0 3.0 2.8 2.6 2.4 2.2 2.0 1.8 A 1.6 k hro - Bi 100 90 80 70 60 50 45 40 35 14 30 Sphere 0.01 0.007 0.005 0.004 0.003 0.002 5 0.001 0 0.5 1.0 1.5 2 2.5 3 4 5 6 78 9 10 20 30 40 50 100 150 200 250 T = atr (a) Midpoint temperature. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. Tx h Initially T=T Tx h 0 % r Q Qmax 1.0 Bi=hrolk 0.9 0.8 0.7 0.6 0.5 - 12 | 0.4 B 0.3 0.2 0.1 Sphere 0. 100 10-5 10-4 10-3 10-2 10-1 1 10 10 103 10+ Bir=hat/k T-T = 00 To-Tx 1.0 rlr = 0.2 0.9 0.8 -0.4. 0.7 0.6 0.6 0.5 0.4 0.3 0.8 0.2 0.9 0.1 1.0 0 0.01 0.1 1.0 10 1 = Bi k hr Sphere (b) Temperature distribution. From M. P. Heisler, "Temperature Charts for Induction and Constant Temperature Heating," Trans. ASME 69, 1947, pp. 227-36. Reprinted by permission of ASME International. (c) Heat transfer. From H. Grber et al.