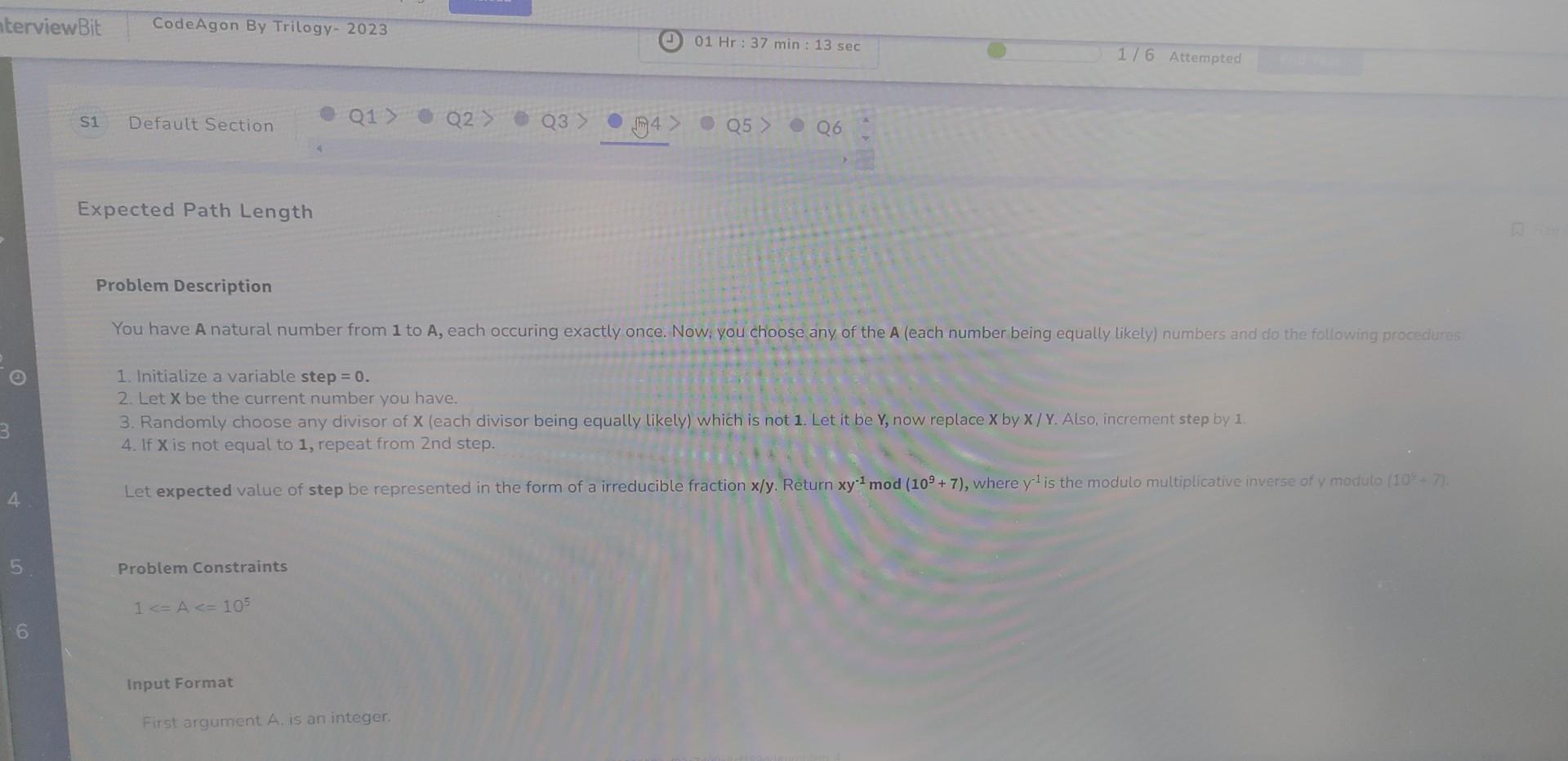
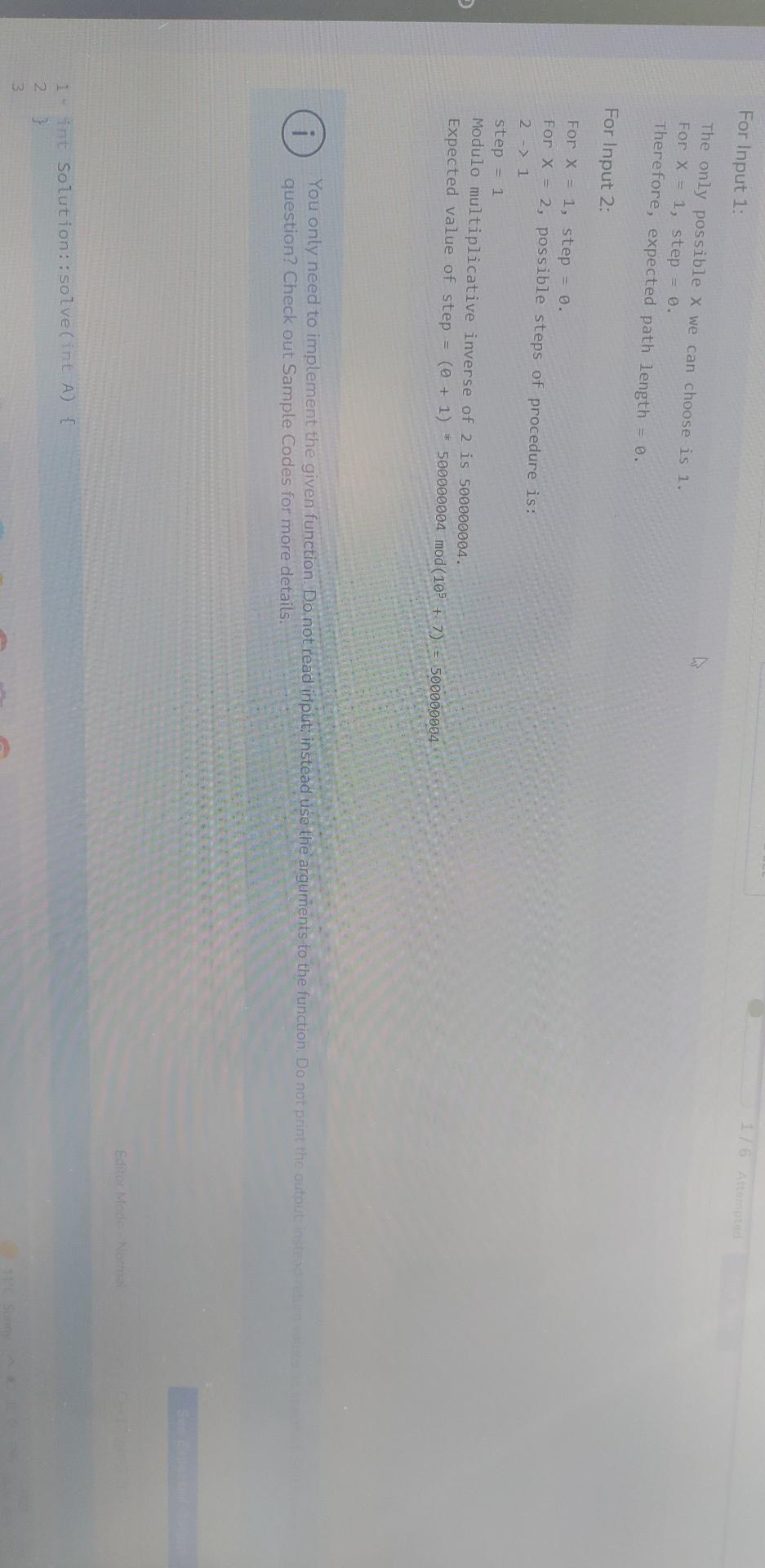
Problem Description You have A natural number from I to A, each occuring exactly once. Now; you choose any of the A (each number being equally likely) numbers and do the following procedures 1. Initialize a variable step =0. 2. Let X be the current number you have. 3. Randomly choose any divisor of X (each divisor being equally likely) which is not 1 . Let it be Y, now replace X by X/Y. Also, increment step by 1 . 4. If X is not equal to 1 , repeat from 2 nd step. Let expected value of step be represented in the form of a irreducible fraction x/y. Return xy1m0d(109+7), where y1 is the modulo multiplicative inverse of y modulo (109+7). Problem Constraints 1=A=105 Input Format First argument A, is an integer. Output Format Return a single integer. Example Input Input 1: A=1 Input 2: The only possible x we can choose is 1 . For x=1, step =0. Therefore, expected path length =0. For Input 2: Forx=1,step=0. For x=2, possible steps of procedure is: 21step=1 Modulo multiplicative inverse of 2 is 500000004 . Expectedvalueofstep=(+1)500000004mod(10+7)=500000004 You only need to implement the given function. Do not question? Check out Sample Codes for more details