Problem:

The source Alphabet is A={a,b,c}. The symbol counts are n_a=16, n_b=2, n_c=2 . You have to encode the sequence ccba using the incremental arithmetic coding algorithm. Show your work for every step: calculate intervals, indicate the bits shifted to the code sequence if any, indicate what type of scaling is applied (E1, E2, E3) if any; E3 counter (if E3 is applied).

.

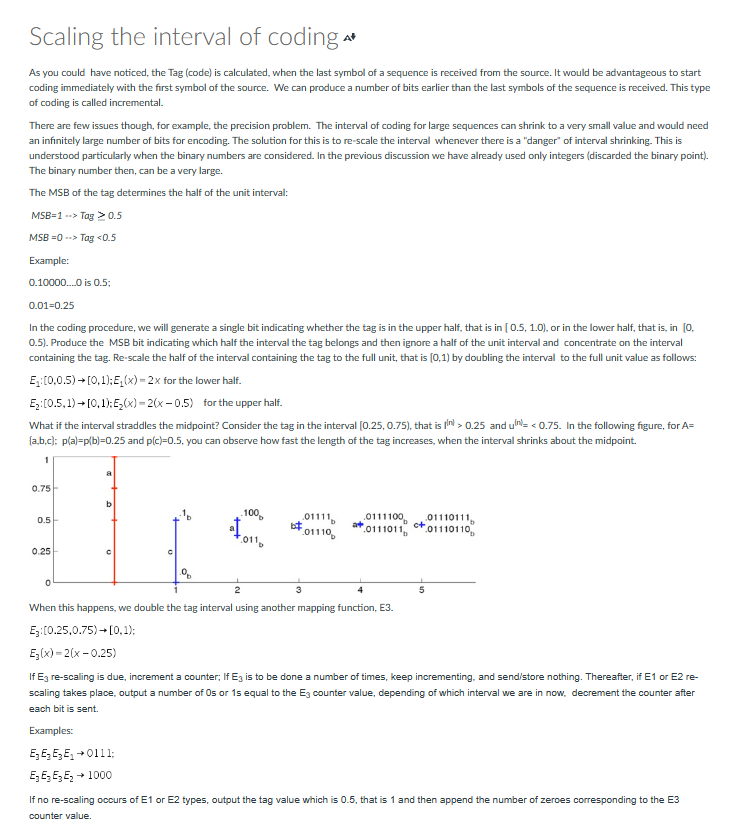
Integer Implementation s* For integer implementation, we use rather counts of occurrences of each symbl, ni. Cumulative counts (Cum_Count) per symbol play the role of the cdf, that is, we use an estimated value of cdf. For the k-th symbol \[ F_{x}(k)=\sum_{i=1}^{k} \frac{n_{i}}{\text { Total_Count }} \text {, } \] where \[ \text { Cum_Count }(k)=\sum_{i=1}^{k} n_{i} \] Calculation of intervals is refined to carry out arithmetic such that the uniqueness of codewords are guaranteed. \[ \begin{array}{l} l^{(n)}=l^{(n-1)}+\left\lfloor\frac{\left(u^{(n-1)}-l^{(n-1)}+1 ight) \times \text { Cum_Count }\left(x_{n}-1 ight)}{\text { Total_Count }} ight floor \\ u^{(n)}=l^{(n-1)}+\left\lfloor\frac{\left(u^{(n-1)}-l^{(n-1)}+1 ight) \times \text { Cum_Count }\left(x_{n} ight)}{\text { Total_Count }} ight floor-1 \\ \end{array} \] where xn is the nth symbol in the alphabet to be encoded. Please note that we round down in the above equations. Since we care about getting the tag in quarter of the unit interval (not lesser as we do re-scaling), the total number of bits for representing the tag, m is calculated from the logarithm of what is four times greater than the total count of symbols in the sequence. Recall, the latter represents in integer arithmetic the complete unit interval. 2m>4 Total_Count Or \[ m>2+\left\lceil\log _{2}(\text { Total_Count) }) ight. \] For example, for the total number of symbols in the message/file to be encoded is 230 , the number of binary digits for represting the tag is to 10. The complete coding algorithm is formalized below: Initialize I and u. Get the symbol, update the interval: \[ \begin{array}{l} l \leftarrow l+\left\lfloor\frac{(u-1+1) \cdot \operatorname{Cum}_{-} \operatorname{Count}(x-1)}{\text { Total_Count }} ight floor \\ u \leftarrow l+\left\lfloor\frac{(u-l+1) \cdot \operatorname{Cum}_{-} \operatorname{Count}(x)}{\text { Total_Count }}-1 ight floor \end{array} \] while (MSB of u and I are both equal to b or E3 condition holds) if (MSB of u and I are both equal to b ) \{ send b (where b is a bit) This algorithm lends itself to a simple circuit implementation. There is only a bit check and shift operation to be performed. Before going into video examples, a few notes on implementation would help. Let the number of bits needed for tag representation is 6 , the algorithm initializes with I=000000 and u=111111. After reading from the input sequence a symbol, we have to recalculate intervals using Eqs. (**). Few scenarios would help with understanding the implementation: Let the new interval bounds are I=001001 and u=010111. Both I and u are in the low half of the unit interval, so we output 0 that indicates the low interval. At this point we have to perform re-scaling of the interval using the mapping function E1. In integer implementation, the equivalent mapping is by shifting left the binary sequence with shift-in from the right 0 for I and 1 for u. That is, the new interval bounds are I=010010 and u=101111. The interval belongs to [0.25,0.75) that can be recognized by two most significant bits being 01(0.25), which with the binary point added is 0.01 and 10 , that is 0.102= 0.510. Thus, we have to perform E3 mapping. This is performed by flipping the second bit in both / and u, and shift left both with shift-in bits 0 and 1 for low and upper bounds, respectively. The counter for E3=1. New interval values are l=000100 and u=111111. Now, because the interval straddles the midpoint, we are ready to get another symbol. Assume, that after calculating new intervals, 1=001001 and u=001111. As this is an indication of the low half of the unit interval, we output 0 , and because E3 counter is 1 , we then output 1 (opposite to 0). New interval is I= 010010 and u= 011111 . It is in the low half. Output 0, shift again: I=100100 and u=111111. Now, it is in the upper half, so we output 1 (shift left). New intervals are 001001 and u11111. Thus, weare ready to get another symbol. If it were a last symbol, we had to send the tag value, and output 1 (meaning 0.5 ). Aa a matter of fact, we can take any value in the interval, and because the low limit is not included in the previous intervals, we can use that as a tag. So, we take is a great simplifation for the algorithm. Do not be confused with this change. All before, that is taking the midpoint of the interval has been made for proving the theorems. Once it is proved, and we understand that any value in the interval is a valid code, we can use this fact for implementation. As you could have noticed, the Tag (code) is calculated, when the last symbol of a sequence is received from the source. It would be advantageous to start coding immediately with the first symbol of the source. We can produce a number of bits earlier than the last symbols of the sequence is received. This type of coding is called incremental. There are few issues though, for example, the precision problem. The interval of coding for large sequences can shrink to a very small value and would need an infinitely large number of bits for encoding. The solution for this is to re-scale the interval whenever there is a "danger" of interval shrinking. This is understood particularly when the binary numbers are considered. In the previous discussion we have already used only integers (discarded the binary point). The binary number then, can be a very large. The MSB of the tag determines the half of the unit interval: MSB=1Tag0.5MSB=0Tag0.25 and u[n)=