Problem: This program computes instrumentation reliability. Equations for analyzing the reliability of instrumentation can be developed from the study of statistics and probability, where the reliability is the proportion of the time that the component works properly. If a component has a reliability of 0.8, then it should work properly 80% of the time. The reliability of combinations of components can also be determined if the individual component reliabilities are known. In order for information to flow from point a to point b in the series design, all three components must work properly. In the parallel design, only one of the three components must work properly for information to flow from point a to point b.

Series design: a - component 1 - component 2 - component 3 - b

Parallel design:

a

component1

component2

component3

b

In a series configuration, if r is the reliability of a component, and if all three components have the same reliability, then it can be shown that the reliability of the series configuration is . If the reliability of each component is 0.8 (which means that a component works properly 80% of the time), the analytical reliability of the series configuration is ( 0.8^3 ) or 0.512. The series configuration should work properly 51.2% o the time. In a parallel configuration, if r is the reliability of a component, and if all three components have the same reliability, then it can be shown that the reliability of the parallel configuration is 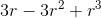. So if the reliability of each component is 0.80, then the analytical reliability of the parallel configuration is 3(0.8) - 3(0.8)^2 + (0.8)^3 or 0.992. The parallel configuration should work properly 99.2% of the time. Your intutituion probably tells you that the parallel configuration is more reliable because only one of the components must be working for the overall configuration to perform properly whereas all three components must work properly in order for the series configuration to perform properly. We can also estimate the reliability of these two designs using a computer simulation based on pseudo random numbers. First, we need to simulate the performance of a single component. If the reliability of a component is 0.8 then it works properly 80% of the time. To simulate this performance, we could generate a random value between 0 and 1. If the value is between 0 and 0.8, then the design works for this one trial; if any one of the numbers is greater than 0.8, then the design does not work for this one trial. If we run hundreds or thousands of trials, we can compute the proportion of the times that the overall design works. This simulation is expected to approximate the analytically computed reliability. To estimate the reliability of the parallel design with a component reliability of 0.8 we again generate three random floating-point numbers between 0 and 1. If any one of the three numbers is less than or equal to 0.8, then the design works for this one trial; if all of the numbers are greater than 0.8, the design does not work for one trail. To estimate the reliability determined by the simulation, we divide the number of trials for which the design works by the total number of trials performed. Develop a program to compare the analytical reliabilities of the series and parallel configurations with simulation results. Allow the user to enter the individual component reliability and the number of trials to use in the simulation. Generate a random number (event) for each component in the simulation; this is a total of 3 random numbers. Use these 3 for the simulation series test and same 3 for simulation parallel test. This will make the simulations an apples-to-apples comparison when evaluating results.

The input/output formats for your program should look like this: Enter individual component reliability: 0.8

Enter in the number of trials: 3

Enter in the unsigned integer seed: 47

Analytical reliability:

Series: 0.512 Parallel: 0.992 Simulation reliability, 3 trials

Series: 0.667 Parallel: 1.000 Additional example of program execution using other test data:

Enter individual component reliability: 0.8

Enter in the number of trials: 100

Enter in the unsigned integer seed: 123 Analytical reliability:

Series: 0.512 Parallel: 0.992 Simulation reliability, 100 trials

Series: 0.470 Parallel: 1.000

Additional example of program execution using other test data:

Enter individual component reliability: 0.8

Enter in the number of trials: 1000

Enter in the unsigned integer seed: 3535 Analytical reliability:

Series: 0.512 Parallel: 0.992 Simulation reliability, 1000 trials

Series: 0.530 Parallel: 0.990

3r-3r2 + r